前面的证明五不好理解,我们改进一下。
在任意一个坐标系内,从原点发射一束光,到达三维坐标轴上任意一点\((x,y,z)\),满足:
\((ct)^2=x^2+y^2+z^2 \)
如果坐标系O’沿着x轴方向相对于坐标系O以匀速\(v\)运动,那么在两个坐标系原点重合时,发射一束光,那么,由于在y和z方向上没有相对运动,所以y,z方向上光走的距离是相同的,假设光到达点\((x,y,z)\)时,O坐标系测得时间为t, O’测得时间为t’,那么必然有:
\((ct)^2-x^2=(ct’)^2-x’^2 \)
x和x’为光在O和O’坐标系的x轴上的坐标值(投影值)。
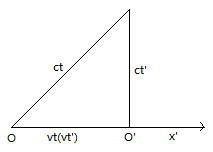
我们知道,光走了t距离时,坐标O’的原点\(x’=0\),而在O上看来,O’的原点在\(x=vt\),也就是光在O和O’上的x坐标上的投影是\(vt\)和0,(O’坐标觉得自己走了\(vt’\)距离),如下图:
于是根据前面的等式,我们可以得到:
\( (ct)^2 - (vt)^2 =(ct’)^2 -0^2 \)
于是得到:
\(t =\gamma t’ \)
于是有:
\( vt =\gamma vt’ \)
上面的等式说明,光在O坐标系内的x方向走了\(vt\),那么在O’上走的距离为\( vt’=vt/\gamma \),由于t是连续的,那么在两个坐标上的任意一点,我们可以肯定,使用同一束光测量的同一个位置,O上的x投影值始终是O’上值的\( \gamma \)倍。
那么我们在O’上寻找一个点,相对于O’原点的坐标为\(x’\),如上图。同样O和O’重合时发射一束光,光在O’坐标系到\(x’\)时,走了\(x’+vt’\)的距离,对应着O坐标系上的\(x\)值,前面我们得出了两个坐标值始终为\( \gamma \)倍关系,所以必然有
\( x=\gamma(x’+vt’) \)。