推迟势中的坐标系关系(下图rR’得x位置是错误的):
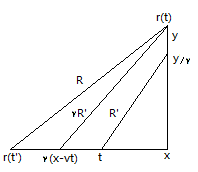
其中:
\( R = \sqrt{(x - vt’)^2 + y^2 + z^2} \)
\( R’ = \sqrt{(x - vt)^2 + \frac{y^2 + z^2}{\gamma^2}} \), 或:\( \gamma R’ = \sqrt{(x - vt)^2 \gamma^2 + y^2 + z^2} \),
其中 \( \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \)
求解过程如下:
电荷q在位置\( r’(vt’,0,0,t’) \)处发出光子,到达点\( r(x,y,z,t) \),
此时满足关系: \( c(t-t’)=R=\sqrt{(x - vt’)^2 + y^2 + z^2} \)
于是可以得到t和t’的关系: \[ t=t’+\sqrt{(x - vt’)^2 + y^2 + z^2}/c \\ t’ = \frac{c^2 t - x v - c\sqrt{(x - v t)^2 + (1 - v^2/c^2)(y^2 + z^2)}}{c^2 - v^2} \]
我们还要求出t和t’的变换率对比,所以使用上式对t’求导:
\(f(t’)=t’+\sqrt{(x - vt’)^2 + y^2 + z^2}/c\)的导数为:
\(f’(t’)=1-\frac{v(x-vt’)}{cR}=\frac{c^2(t-t’) - v(x-vt’)}{cR}\),
将前面求出的t’代入f’(t’),就能得到:
\( f’(t’)= \frac{\sqrt{(x-vt)^2 + (1-\frac{v^2}{c^2})(y^2+z^2)}}{R}\)
也就是: \( \frac{\Delta(t)}{\Delta(t’)}=\frac{R’}{\gamma R}\)
\(R’=\sqrt{\gamma^2(x-vt)^2 + (y^2+z^2)}\),
\(R=c(t-t’)=\sqrt{(x-vt’)^2 + (y^2+z^2)}\), 将t’代入得:
\( R=\frac{c(-v^2 t + x v) + c^2 \sqrt{(x - v t)^2 + \left(1 - \frac{v^2}{c^2}\right)(y^2 + z^2)}}{c^2 - v^2} \)
\(\gamma=\sqrt{\frac{1}{1-v^2/c^2}} \)
由\(t=t’+R/c\),可得:
\( \frac{dt}{dt’}=1+\frac{1}{c}\frac{dR}{dt’}\),继续:
\( =1-\frac{v(x-vt’)}{cR}=\frac{R-\frac{v}{c}(x-vt’)}{R}\)
我们让\(t’=0\),表示从原点发出的光,从原点开始计时,那么:
在静止坐标系内观察:
\(R=ct=\sqrt{x^2 + y^2 + z^2}\),
在粒子自己的坐标系内观察:
\(R’=\sqrt{\gamma^2(x-vt)^2 + y^2 + z^2}=\sqrt{x’^2 + y^2 + z^2}\),
注意,因为不存在y,z方向的运动,所以两个坐标系的y,z大小是不变的,
于是我们可以得到洛伦茨变换的对应关系:
\( x’=\gamma(x-vt) \)
同时有:\( \frac{dt}{dt’} =\frac{R-\frac{v}{c}x}{R} \)
也就是在发射光子的电荷位置\( r’(x’,0,0,t’) \),与接收到光子的任意位置\( r((x,y,z,t) \),其x的位置变化速率是不同的,关键原因就是光子从r’到r是有时间的,所以就出现了r和r’并不是同步的情况,如果没有时间延迟,那么r和r’将会整体平移。如下图:\(|AB|=\gamma|A’B’|\)
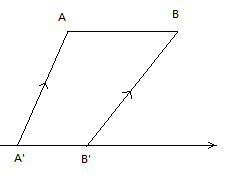
这也是狭义相对论的一个新解释,也许是最好的解释。