-
飞机停止时,飞机上的原子钟比地球上的原子钟慢了一些时间。按说应该相同。除非在飞机上的1秒和地球上的1秒不同,也就是振荡的频率不同,或者在加速减速过程中时钟有了变化,但这种情况不应该和飞机匀速飞的时长有关,所以应该排除。
-
使用推迟势计算,为什么要保持y不同,才能推迟洛伦兹变换。
-
多普勒效应中,为什么x方向要多一个\(\gamma\),即\(\gamma(1-v/c)\), 正好对应推迟势中的\(\gamma(x-vt)=\gamma(1-v/c)(x-vt’)\),
如果是飞机上的原子钟的1秒和地球上的1秒不同,那么这些问题就都能解决了。
在洛伦兹变换下,推迟势中,R’中的接收时间\(\gamma(t-xv/c^2)\)对应R的t,发射时间\(t’/\gamma\)对应R的t'
=====
在静止坐标系内观察移动坐标系:
\(\Delta t=\frac{x-vt}{c-v}\)
即:\(t_r-t_e=\frac{x-vt_r}{c-v}\)
\(t_e =t_r-\frac{x-vt_r}{c-v}\)
\(=\frac{ct_r-x}{c-v}\)
\(=(ct_r-x)\frac{c+v}{c^2}\frac{c^2}{c^2-v^2}\)
\(=\gamma^2 \frac{ct_r-x)(c+v)}{c^2}\)
\(=\gamma^2(t_r-\frac{vx}{c^2}-\frac{x-vt_r}{c})\)
\(=\gamma(\gamma(t_r-\frac{vx}{c^2})-\frac{\gamma(x-vt_r)}{c})\)
\(=\gamma(t’_r-\frac{x’}{c})\)
\(=\gamma t’_e\)
表示在发射点x’_e为0的时候,\(t_e=\gamma(t’_e+\frac{x’_e v}{c^2})=\gamma t’_e\)
所以上面我们使用到了:
\(t’_r=\gamma(t_r-\frac{xv}{c^2})\)
\(t_e=\gamma(t’_e+\frac{x’_e v}{c^2})\), 光源位置\(x’_e=0\)
\(x’=\gamma(x-vt)\)
这些公式和前面的\(\gamma R’\)相同。这些公式说明了什么?
这个推导过程至少说明了,我们应该使用相同类型的时间来对比,
\(t_e\)对比\(t’_e\), \(t_r\)对比\(t’_r\),
如果我们使用了\(t_e\)对比\(t_r\)或\(t’_r\),那么可能就会丢失\(\gamma\),
使得多普勒变换的频率丢失了\(\gamma\),只是\(dt/dt’\)而不是\(\gamma dt_r/dt_e\)
=======
在移动坐标系内,
\(x’_r-x’_e=c(t’_r-c’_e)\),
光线接收时间\(t’_r\),发射时间\(c’_e\),接收位置\(x’_r\),发射位置\(x’_e\)
有:
\((x’_r - x’_e) (1 - \frac{v}{c}) = (t’_r - t’_e) (c - v)\),
\((x’_r - x’_e)+v(t’_r - t’_e)=c(t’_r - t’_e)+(x’_r - x’_e)\frac{v}{c}\),
\((x’_r + vt’_r)-(x’_e + vt’_e)=c(t’_r + \frac{v x’_r}{c^2})-c(t’_e + \frac{v x’_e}{c^2})\),
\(\gamma(x’_r + vt’_r)-\gamma(x’_e + vt’_e)=c(\gamma(t’_r + \frac{v x’_r}{c^2}))-c(\gamma(t’_e + \frac{v x’_e}{c^2}))\),
即:
\(x_r-x_e=c(t_r-t_e)\)
这个变换说明了世界线的不变量\(c\Delta t-\Delta x=0\)。这个变换的推导又说明了什么?
====
还有一个等式:
\( c^2(t-\frac{vx}{c^2})^2-(x-vt)^2=\frac{(ct)^2-x^2}{\gamma^2}=\frac{y^2}{\gamma^2}\)
也就是从等心圆\(x’^2+y’^2=(ct’)^2\)到等心圆\(x^2+y^2=(ct)^2\)
这个推导的意义,是说明\(t’=t-xv/c^2\)与\(y’=y/\gamma\)是等价的,t的缩减是由于y的缩减造成的,或者t缩减则y缩减了,这个也与光速变成了c/\gamma等价
=====
就是如果令x’=x-vt,那么这个x’并非发射位置,而是瞬时位置,也就是观察点接收到信号后的光源位置, 而我们使用的静止坐标系的x-vt’却是发射位置。这也是长度收缩的原因,在O’系看来,x-vt和x这两个点是发射位置和接收位置,是不同时的,但在O系看来,这两个位置是同时的,x-vt不是发射位置
当然,最重要的一点,是保持了观察点位置的固定,也就是y方向固定,这个是条件
那么怎么根据这句话,推导出在O’坐标系,瞬时位置为x-vt时的发射位置为\(\gamma(x-vt)\),不考虑y值相同的情况
======
我们使用\(c(t’_r-t’_e)=x-v t_r\),假设推迟距离为\(x-v t_r\),
如果再假设不同坐标系的接收时间同步,也就是\(t’_r=t_r\),那么有:
\(c(t_r-t’_e)=x-v t_r\),
有:\(t’_e =t_r-(x-v t_r)/c\), (1)
由于 \(c(t_r-t_e)=x-v t_e\), 有:
\(t_r=t_e + (x-v t_e)/c\), 代入(1), 有:
\(t’_e =t_e+\frac{x-v t_e}{c}-(x-v \frac{t_e+(x-v t_e)}{c})/c \)
有:
\(t’_e =t_e + \frac{v(x-v t_e)}{c^2} =\frac{t_e}{\gamma^2}+\frac{vx}{c^2}\)
\(x’=x-v t’_e=\frac{x-v t_e}{\gamma^2}=\frac{c}{c-v}(x-v t_r) \frac{c^2-v^2}{c^2}=\frac{c+v}{c}(x-v t_r)\)
如果\(x=v t_e\), 此时光线始终垂直于静止坐标系的x轴,
\(t’_e =t_e\)
如果 \(x=vt\), 此时光线始终垂直于移动坐标系的x轴,
\(t’_e =t’_r =t_r\),
\(t_r-t_e =\frac{x-v t_e}{c}=\frac{v}{c}(t_r-t_e)\)
有:\(t_r=t_e\)(垂直发射), 或\(v=c\)(光子)
由于始终有 \(c(t’_r-t’_e)-(x-v t_r)=c(t_r-t_e)-(x-v t_e) =0\),
所以一维情况下,是无法得到\(\gamma\)的,也就是在无源的波动方程里,没有y方向的波动方程里,是不能得到\(\gamma\)放大参数的,O’坐标系的\(t’_r t’_e\)可以无限制放大,只有引入y做限制,才有\(\gamma\)的出现。除非我们追求变换的统一性,在t’到t的变换和t到t’的变换里,参数是一样的,都是\(\gamma\),就可以找到这个共同的放大参数。
=== 我们找到统一使用接收时间的变换
\(c(t’_r-t’_e)=x-v t_r\),
假设发射时间相同,\(t’_e =t_e\), 则有:
\( t’_r=t_r-\frac{v(x-v t_e)}{c^2}\)
\(x’=x-v t_r=x-v t_e-v(t_r-t_e)\),
\(x-v t_e\)作为\(x\),\(t_r-t_e\)作为\(t\),
\(x-v t_r\)作为\(x’\),\(t’_r-t_e\)作为\(t’\),
有:
\( t’_r-t_e=t_r-t_e-\frac{vx}{c^2}\), 即:
\( t’=t-\frac{v x}{c^2}\)
\( x’=x-vt\)
其反变换:
\( t=\gamma^2(t’+\frac{v x’}{c^2})\),
\( x=\gamma^2(x’+vt’)\),
或写作:
\((t’_r - t’_e) = (t_r - t_e) - \frac{v (x - v t_e)}{c^2}\)
\((t_r - t_e) = \gamma^2 \left( (t’_r - t’_e) + \frac{v (x - v t_r)}{c^2} \right)\)
所以,我们为了让变换统一,需要将t’和x’的变换里扩大\(\gamma\)倍,此时t和x的变换就缩小了\(\gamma\)倍,两者就统一了,这是在一维变换下一个能得到增大\(\gamma\)的理由。
当然,如果\((ct’)^2-x’^2\)和\((ct)^2-x^2\)不为0,则可以得到:
\((ct’)^2-x’^2=\frac{(ct)^2-x^2}{\gamma^2}\), 而这在现实中,只要不是光子,就肯定两者不为0
==== 我们继续使用二维含y的方程来推导\(\gamma\):
\(c(t_r-t_e)=R=\sqrt{(x-v t_e)^2+y^2}\)
\(c(t’_r-t’_e)=R=\sqrt{(x-v t_r)^2+y’^2}\)
我们假设两个坐标系使用同一个发射时间,\(t_e=t’_e\)求出 \(t’_r\)于\(t_r\)的关系式:
\( t’_r=t_r-\frac{v(x-v t_e)}{c^2}\), 和一维的完全一样
但此时有y,我们有:
\((c(t’_r-t_e))^2-(x-v t_r)^2 =\frac{(c(t_r-t_e))^2-(x-v t_e)^2}{\gamma^2}=(y/\gamma)^2\)
可见,为了让y相同,在二维情况下,我们需要将整个移动坐标系下的\(t’_r\), \(t’_e\), \(x’\)都扩大\(\gamma\)倍:
\(\gamma t’_r=\gamma(t_r-\frac{v(x-v t_e)}{c^2})\)
\(\gamma t’_e =\gamma t_e \)
\(\gamma x’ =\gamma(x-v t_r)\)
即:
\(\gamma c(t’_r-t_e)=\gamma R=\gamma \sqrt{(x-v t_r)^2+y’^2}=\sqrt{(\gamma(x-v t_r))^2+y^2}\)
====
再考虑一维情况:
假设移动坐标系内推迟位置为\(a(x-v t_r), a>1\), 则有
\(c(t’_r-t’_e)=a(x-v t_r)=x’-v t’_e\),
我们先要找到一个合理的x':
令\(a=\gamma\),于是:
\(\gamma (x-v t_r)=x’-v t’_e\), 得到:
\( x’=\gamma(x-v t_r)+v t’_e \)
前面我们有:
\(c(\gamma(t_r-\frac{v (x-v t_e)}{c^2})-\gamma t_e)=\gamma(x-v t_r)\),
所以令\(t’_e =\gamma t_e\),得到:
\( x’=\gamma(x-v t_r)+v\gamma t_e=\gamma(x-v(t_r-t_e)) \)
可见,x’是从\(x-v(t_r-t_e)\)也就是移动坐标系的原点坐标,扩大了\(\gamma\)倍得到的
可见,整个系统都扩大了\(\gamma\)倍,包括移动坐标系的原点在静止参考系内的坐标!
于是,我们前面的方程就变成了:
\(c(t’_r-t’_e)=\gamma (x-v t_r)=\gamma(x-v(t_r-t_e))-v t’_e\),
由\(\gamma (x-v t_r)=\gamma(x-v(t_r-t_e))-v t’_e\),
可以得到:\(t’_e=\gamma t_e \)
再由\(c(t’_r-t’_e)=\gamma (x-v t_r)\),
可以得到:\(t’_r=\gamma(t_r-\frac{v (x-v t_e)}{c^2}\),
我们再使用式子:
\(c(t’_r-t’_e)=A (x-v t_r)=A(x-v(t_r-t_e))-v t’_e\),
可以得到:
\(t’_e=A t_e \)
\(t’_r=A(t_r-\frac{v (x-v t_e)}{c^2}\)
可见\(\gamma\)只是和普通缩放一样,并没有特殊性
这可能说明,系统内有不变量,体现在\(c(t_r-t_e)\)与\(x-v t_e\)的差值中,光子不变量为0,费米子不变量大于0,快子不变量小于0,电磁场不变量是电荷和静电场,质量不变量是静质量。
而从\((c-v)(c+v)=(c/\gamma)^2\),似乎可以得到什么启示,这好像是一种什么振荡模式。在粒子获得速度v后,y方向的光速必须降低为\(c/\gamma\)才能保持光速不变,但水平方向上却要用\((c-v)(c+v)\)来体现,很是奇怪。
====
如何在一维下构造二维的y分量从而找到\(\gamma\),或者找到某个同时性的事件,但如果没有y,那在x轴上任意放大都能做到(x,y=0)点上可以同时。
前面我们假设\(t_e =t’_e\)时, 得到
\(t’_r=t_r-v(x-v t_e)/c^2\),
假设:\(c(t’_r-t_e))^2-(x-v t_r)^2\) 和\((c(t_r-t_e))^2-(x-v t_e)^2\) 都不等于0
可得 \((c(t’_r-t_e))^2-(x-v t_r)^2=(1-v^2/c^2) ((c(t_r-t_e))^2-(x-v t_e)^2)\),
\(c(t’_r-t_e)+(x-v t_r)=(1-v/c)(c(t_r-t_e)+x-v t_e\)
\(c(t’_r-t_e)-(x-v t_r)=(1+v/c)(c(t_r-t_e)-(x-v t_e)\)
得:
\(c(t’_r-t_e)=c(t_r-t_e)-\frac{v}{c}(x-v t_e)\),
\(x-v t_r=x-v t_e-\frac{v}{c} c(t_r-t_e)\),
此时,再考虑为什么要扩大\(\gamma\)倍,
从上面的公式,我们很容易就知道其几何图像,如下图:
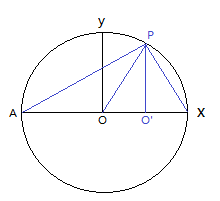
从这个图可以看出,
在产生速度v后,相当于所有的圆半径r都倾斜,变成了新的方向,
比如图中有向倾斜的半径OP,可以看作是垂直半径OY,静止时垂直速度为c,运动时向运动方向倾斜产生了速度v,
为了保持光速不变,实际上也是半径r的长度不变(代表势能不变,由此可以想象出光速是势能除以距离得到的常数),垂直方向变成了\(\sqrt{c^2-v^2}\),水平方向产生了速度v,
在圆里面,三角形APX是直角三角形,O’P垂直于AX, 那么OP代表\(c(t’_r-t’_e)\), OO’代表\(x-v t_r\), O’X就代表\(c(t’_r-t’_e)-x-v t_r\), AO’就代表\(c(t’_r-t’_e)+x-v t_r\),
于是根据图片内直角三角形APO’和PO’X的相似关系,就有:
\(\frac{O’X}{O’P}=\frac{O’P}{AO’}\), 于是可以得到:
\((c(t’_r-t’_e)-x-v t_r)(c(t’_r-t’_e)+x-v t_r))=(O’P)^2=y’^2\)
也就是以O’P形成了一个新的小圆。而这个小圆x方向上虽然左右不均匀,但整体上乘积却是和圆一样,这意味着什么?
在x方向的光线如何变化呢?
我们可以看作x方向的光线,是OP无限靠近x轴的结果(这也说明是v趋于c,变成光子),
所以,在x方向上,我们也可以看作是y趋于0,即\(c(t’_r-t’_e)\)趋于\(x-v t_r\),此时相当于v趋于c。当v等于c时,也就是光子的运动,这不是我们要讨论的情况,我们讨论的是小于c的粒子的运动,所以永远有v小于c,\(c(t’_r-t’_e)-(x-v t_r)\)始终不为0。
向右的距离*向左的距离=\(\gamma(c-v)\Delta t’ * \gamma(c+v) \Delta t’=c^2 \Delta t’^2=\Delta x’^2\),
在O’中从原点向左右发射两束光,在t’时刻到达x’,-x’, 静止左边系内的t和x’,-x’对应的坐标:
x’对应:
\(x_A = \gamma (c + v) t’ \)
\(t_A = \gamma \left(1 + \frac{v}{c} \right) t’\)
-x’对应:
\(x_B = \gamma (v - c) t’ \)
\(t_B = \gamma \left(1 - \frac{v}{c} \right) t’\)
\(x_A*x_B=x’^2\)
\(t_A*t_B=t’^2\)
代表了逆变换关系,没有\gamma则逆变换不成立,这也是y相同的结果。但在现实中的含义是什么:
上面的图片中,我们看到:
\(O’X=OX-OO’=r-vt=r(1-v/c)\), \(r=ct\)
\(O’A=r(1+v/c)\), \(r=ct\)
\(O’X * O’A=(\frac{r}{\gamma})^2\)
我们认为,移动坐标系原点在O位置时发射信号,这个信号强度与半径r成比例,比如势能是成反比,
此时的等势面就是范围r的圆周,假设信号强度为m(r),
信号不断向外扩散,在坐标原点移动到O’时,在垂直位置\(O’P=\frac{r}{\gamma}\)正好收到斜率为v/c的信号m(r),如果信号强度与r成反比例,则在O’中与O中的等势面要扩大\(\gamma\)倍,\(r’=\gamma r\),扩大后有:
\(\gamma O’X * \gamma O’A=r^2\)
那么在x方向,是否存在这种等势面?
在x轴正方向,m(r)在O’移动vt后,相对于O’的距离为r(1-v/c),这显然不同于垂直方向的\(\gamma\),
在x轴负方向,m(r)在O’移动vt后,相对于O’的距离为r(1+v/c)。
由回到前面的问题,水平方向上,\((c-v)*(c+v)=c^2-v^2\)意味着哪个不变量?为什么等同于垂直的圆的面积\((\frac{r}{\gamma})^2\)一样?
我们看看O坐标系内的圆\(x^2+y^2=r^2\),在O’中变成了方程:
\((x-vt)^2+(y/\gamma)^2=r’^2=(ct)^2\)
椭圆的面积:
\((ct)(ct/\gamma)^2 =(\frac{r}{\gamma})^2\)
而 \(ct(1-v/c) * ct(1+v/c)\)也正好等于\(\frac{r}{\gamma}^2\),这也说明了在O看来是椭圆,但在O’看来,是半径为\(\frac{r}{\gamma}\)的标准圆,保持各向同性。
O’的垂直轴将椭球切成了\(x’=r(1-v/c)\)和\(x’=-r(1+v/c)\)两部分,x方向的直径仍然为2*r,也就是从整体上来看,x方向没有压缩,但中心发生了偏离为\((-\frac{v}{c}r,0)\),y方向则压缩了\(\gamma\)。也就是等势面变成了一个x半径为\(r’=r=ct\)不变,y方向变成了\(r/\gamma\)被压缩了\(\gamma\)倍的椭圆,y方向的密度增加,x方向的不变但位置发生了偏移。
也就是我们前面要找的两个值为什么相等,实质上是面积为不变量。
再乘以\(\gamma\),使得面积等于\(r^2\),x方向空间增加了\(\gamma\)倍,y方向空间不变,x方向相同距离势能不变(相对于中心),y方向相同距离势能增加了\(\gamma\)倍(在\(y’=y\)位置变成了\(\gamma m(r)\))。
等势面,也可以看作“同时面”,也就是光源在某个时刻向四周发射光,能同时看到这个发光事件的人的所有可能位置,在静止坐标系内发射,看到的是半径为r的圆,在静止坐标系内看运动坐标系发射,则看到的是y方向压缩的椭圆,在静止坐标内自己看,是一个半径\(r/\gamma\)的小圆。
=====
在电荷运动中,我们用这个来计算一下电场和磁场:
电荷运动后,等势面变成了:
\(x^2+y/\gamma^2=r’^2=(ct’)^2\),
x方向不变,y方向增强\(\gamma\)倍,即:
\(E’^2=E_\parallel^2 +E_\perp^2 \gamma^2\)
\( =E_\parallel^2 + E_\perp^2 \frac{c^2}{c^2-v^2}\)
\( =E_\parallel^2 + E_\perp^2 (1+\frac{v^2}{c^2-v^2})\)
\( =E_\parallel^2 + E_\perp^2 (1+\frac{v^2}{c^2}\frac{c^2}{c^2-v^2})\)
\( =E_\parallel^2 + E_\perp^2 +E_\perp^2 \frac{v^2}{c^2}\gamma^2\)
\( =E^2 + (cB’)^2\)
其中\(B’=E_\perp \frac{v}{c^2}\gamma\)
如果使用坐标变换来进行电磁场变换,也就是上面的反变换,则变成了y方向不变,y方向势能不变,x方向坐标扩大\(\gamma\)倍导致势能缩小\(\gamma\)倍,电场变为:
\(E^2 =\frac{E’_\parallel^2}{\gamma^2}+E’_\perp^2\)
\(= \frac{E’_\parallel^2}{\gamma^2}+E’_\perp^2(\frac{c^2-v^2}{c^2}+\frac{v^2}{c^2})\)
\(= \frac{E’_\parallel^2}{\gamma^2}+\frac{E’_\perp^2}{\gamma^2}+E’_\perp^2\frac{v^2}{c^2}\)
\(= \frac{E’^2}{\gamma^2}+E’_\perp^2\frac{v^2}{c^2}\)
\(= \frac{E’^2}{\gamma^2}+(cB)^2\)
在两边乘以\(\gamma\),即变回缩小的形式:
\(\gamma^2 E^2= E’^2+(\gamma cB)^2\),
或:\(E’^2= E_0^2+(vB’)^2\)
这个也是质能方程相似的形式
根据\(r’=(x-vt)^2+(y^2+z^2)/\gamma^2\)构造势能函数,比如李纳维谢尔势函数,就可以求出其散度和旋度,验证麦克斯韦方程组
====
我们一直在研究:
\(R’=\sqrt{(x-v t_r)^2+y^2/\gamma^2}\),与它的反方向变换:
\(R’_2=\sqrt{(x+v t_r)^2+y^2/\gamma^2}\),
它们两个组成了一个椭圆,圆心在\((-v t_r, 0)\):
\((x-v t_r)(x+v t_r)=(y/\gamma)^2\)
但这个变换并不能让我们找到x方向的\(\gamma\)扩大的理由。
我们显然忽视了一条真正的线,就是在静止坐标系里看到的观察点到当前光源的那条线:
\(R_1=\sqrt{(x-v t_r)^2+y^2}\), 似乎走不通。
====
\((c-v cos())^2 + (\gamma^2 v^2 /c^2) *(c cos()-v)^2 =\gamma^2 (c-v cos())^2-v sin^2()\)
\((c-v cos())^2 + (\gamma^2 v^2 /c^2) *(c cos()-v)^2 + v sin^2()+(c sin()/\gamma)^2 = \gamma^2 (c-v cos())^2+(csin())^2\)
\(v sin()\)是v到c的投影的垂线,如果丢掉,y就变成\(y/\gamma\),
但\(\frac{\gamma v}{c}(c cos()-v)\)是什么,如果丢掉,x方向就是\(c cos()-v\)
\((\gamma(c-v cos()))^2= (c sin()/\gamma)^2 +(v sin())^2 + (c cos()-v)^2 + (\gamma v(c cos()-v)/c)^2\) == 在O上观察O’的光:
\(((c-v cos(\theta)))^2 - (c cos(\theta)-v)^2 = \frac{csin(\theta)}{\gamma})^2 \)
y方向的速度降低了\(\gamma\)倍
== 在O’上观察O的光:
\(((c+v cos(\theta’)))^2 - (c cos(\theta’)+v)^2 = \frac{csin(\theta’)}{\gamma})^2 \)
y方向的速度也降低了\(\gamma\)倍
光源在剔除了vy/c后,方向是如何发射偏折的/折射。折射率:
\( cos(\theta’)=\frac{c cos(\theta)-v}{c-v cos(\theta)}\)
\(sin(\theta)=\gamma sin(\theta’)(1-\frac{v}{c}cos(\theta))\)
令\(c’=\sqrt{c^2-v^2}\),
\(\frac{\sin\theta}{\sin\theta’}=\frac{y}{R}/\frac{y}{\gamma R’}=\gamma (1-\frac{v}{c}\cos\theta)=\frac{c}{c’}(1-\frac{v}{c}\cos\theta)\)
\(\frac{\sin\theta’}{\sin\theta}=\gamma (1+\frac{v}{c}\cos\theta’)\)
\(\frac{\sin\theta}{\sin\theta’(1-v\cos\theta)}=\gamma=\frac{c}{c’}\)
说明折射是光速变化,光进入不同密度,光源移动的三种等价描述,光速变化是因为光的相对观察方向变化了。
\(R^2(1-v\cos\theta/c)(1-v \cos\theta’)=(x-vt_r)^2+y^2\)
\(c’_x= (c \cos\theta-v)/(1-v\cos\theta/v)\)
\(c’_y= c \sin\theta/(\gamma (1-v\cos\theta/v))\)
\(1 - \frac{v}{c} \cos\theta’ = \frac{1 - (v/c)\cos\theta - (v/c)(\cos\theta - v/c)}{1 - (v/c)\cos\theta}\)
\(= \frac{(1 - v/c \cos\theta)^2 + (v^2/c^2)\sin^2\theta}{1 - (v/c)\cos\theta}\)
\(cos(\theta)-cos(\theta’)=v/c \sin^2\theta/(1-v/c \cos\theta)=v/c \sin^2\theta R/R’=v/c * y\sin \theta/R’\)
角度变化,是因为光的速度,\(y\)方向变化速度为从\(c \sin\theta\)到\(c \sin\theta/\gamma\), \(x\)方向是从\(c \cos\theta\)变成了\(c \cos\theta-v\),两个方向变化速度不同
但是如何从几何作图上来直观表现y方向的变化和新的三角形关系?R’=R(1-v/c cos()),O’到R’的垂线是vcos,vsin, 如何知道O’移到垂足后,垂直方向减去的vsin,就是y方向三角形的一个分量,从几何作图上很难做出两者的关系,只能从vsin,c-vcos,csin,ccos-v四条边构成的四边形来计算得出,如果将vsin移到y边上直观体现四者的关系?
洛伦兹变换和伽利略变换的区别,在x方向的运动者观察运动物体A,伽利略变换认为运动物体A的y方向的速度不变,而洛伦兹变换则认为运动物体的y的速度变成了\(y/\gamma\),伽利略用的是想象中的绝对时空,洛伦兹变换则是用了光计时和光测距的相对时空。运动导致的光线偏折,牵涉到光路变化的测量问题、势能等势面的变化、时钟频率的变化、发射时间和接收时间的不同步等等所有相对论问题
====
如果将\(c \cos\theta\) 和\(c \sin\theta/\gamma\)都除以\((1-v \cos\theta/c)\), 就恢复到了对应R的偏移速度,合成速度就是c了
\(\frac{c \sin\theta}{\gamma(1-v\cos\theta)/c)}=\frac{cy}{\gamma R’}=c\sin\theta’=c_{y’}\)
\(\frac{c \cos\theta-v}{1-v\cos\theta/c}=\frac{c(x-vt_r)}{R’}=c\cos\theta’=c_{x’}\)
假设\(c_{y’}*t=y\), 有\(t=\frac{y}{c_{y’}}\),
有:
\(c_{x’}*t =c_{x’}*\frac{y}{c_{y’}}=y\frac{\cos\theta’}{\sin\theta’}\)
\(=y\gamma\frac{\cos\theta-v/c}{\sin\theta}\)
\(=y\gamma \frac{R(\cos\theta-v/c}{R\sin\theta}\)
\(=y\gamma\frac{x-v t_r}{y}\)
\(=\gamma(x-v t_r)\)
相对于把\(y/\gamma\)扩大到y。可见真实的速度应该是将\(ccos-v\)和\(y/\gamma\) 再除以\(1-v \cos\theta/c\)映射回O坐标系,使得其作为原来的\(c_x=ccos\)和\(c_y=csin\)在倾斜后仍保持合成光速不变。
\(\gamma\)最终来自y轴的不协调,所以只需要将\(\gamma\)的研究集中在为什么在y轴产生即可。
为什么要除以\(1-\frac{v}{c}\cos\theta\)?
这个我们可以从以前分析一维的情况下得到为什么是除以它,
在一维情况下,我们有:
\( x-v t_r=(c-v)(t_r-t_e)\),
相对于在O’中,光走了\(x-v t_r=(c-v)(t_r-t_e)\),
也就是我们可以认为,光在O’中的速度为(c-v),与光速比例为(c-v)/c,
而要得到在O’中也是光速的结论,
我们需要将时间也降到(c-v)/c=1-v/c的比例,
我们使用 \(\frac{(c-v)\Delta t}{\Delta t’}=\frac{(c-v)\Delta t}{\Delta t(1-v/c)}=c\),
而\(1-v/c\)正是一维情况下的接收时间对发射时间的导数:
\(\frac{dt_r}{dt_e}=1-\frac{v}{c}\),此导数由\( x-v t_r=(c-v)(t_r-t_e)\)即可得到,
说明测量者观察到的是接收时间间隔,反映了在观测位置,光源因运动导致了不同时刻发出的光的距离的压缩情况,接收时间间隔和发射时间间隔不同造成了观测效应的不同。比如,你在t1时刻发射了一束光,你的速度也是光速,那你沿着光束一样的方向前进,那么发射的光束永远和你并排前进,你在任意时刻t2发出第二束光,它们之间的距离和时间间隔永远是0,
所以在x轴看,O’坐标到x位置走了\((c\cos\theta-v)(t_r-t_e)\)的距离,
再除以接收时间间隔\((t_r-t_e)\frac{dt_r}{dt_e}=(t_r-t_e)(1-\frac{v}{c}\cos\theta)\),就是在O’中的速度\(\frac{c \cos\theta-v}{1-v\cos\theta/c}\),即 \(c’=\frac{\Delta x’}{\Delta t’}=\frac{(c\frac{dt_r}{dt_e}) \Delta t}{\Delta t \frac{dt_r}{dt_e}}=c\),
在观察者看来,光源和光不仅存在x轴的相对速度的变化\(c \cos\theta-v\),还存在光线方向的接收时间的变化,这两个变化成正相关关系,静止系内看相对速度变小(\(c’_x=c\cos\theta-v\)),结果造成接收端距离变小,同时相对接收时间间隔变小(\(t’=t(1-v\cos\theta/c)\)),组合在一起则形成了光速不变(还要和y轴一起)。也就是,观测者是以接收到的事件的时间和距离间隔为准,以接收端的信息为准
之所以消去了\(vsin(\theta)\)项得到了\(csin(\theta)/\gamma\),是因为从光源做垂线到光轴,垂足的位置,就是减去了v和vsin的结果。减去后,就从O’P这个伽利略变换的O’到观察点的即时位置,变换回了R这个洛伦兹变换的推迟位置。
而之所以不使用\(c\cos\theta(1-vcos\theta/c)\)和\(c\sin\theta(1-vcos\theta/c)\)来作为O’系的速度分量,是因为观察时测量的是光源的瞬时位置,这时候x方向的速度就应该使用\(c\cos\theta-v\),y方向的相对速度计算可得为\(\sin\theta/\gamma\),再除以(1-v\cos\theta)就可以得到速度修正。这也是伽利略变换和洛伦兹变换的区别:我们进行速度变换时,伽利略变换使用的是光的延迟发射位置,洛伦兹变换使用的是当前的真实位置(时间不确定时至少角度是真实的)。
也就是,计算距离时,我们用的是相对速度*发射时间间隔=光速*接收时间间隔,计算时间时我们用的时接收时间间隔,所以距离/时间仍然是光速
这也说明了,x和y方向的变换是独立的,y方向遵从\(y,vy/c,y/\gamma\)三角变换。
令\(\cos\theta=v/c\),则:
\(\tan\frac{\theta’}{2} \tan\frac{a}{2} = \tan\frac{\theta}{2}\)
即\(\frac{1-\cos\theta’}{1+\cos\theta’}\frac{1-v/c}{1+v/c}\frac{1-\cos\theta}={1+\cos\theta}\)
由于x和y方向变化率的不同,观测者观察到的光的方向,和粒子发射的光的方向,是不同的,导致了和折射一样的效果,即从O’到观察点的位置,到R这个虚拟位置,水平方向和垂直方向减去了v的影响后得到了R’。
也就是,假设水中的光速,x方向降低了v变成了\(ccos-v\), y方向降低了vsin变成\(csin/\gamma\),那么外部观察到的鱼的角度是\(\theta\),其实鱼的真实角度是在\(\theta’\)
===== 经过艰苦的寻找,最终找到\(\gamma\)的计算方法:
\(\gamma\)的出现,源于\(\partial R/\partial y=-c \partial t_e/\partial y=csin/(c-vcos)\),和\(R’=R-v(x-vt_e)/c\),从而能根据tan(\theta’)等于y的梯度处于x的梯度,得出新角度值。
也就是,在观察点固定,发射时间变化的时候,发射时间的梯度与R的方向高度相关,也就导致发射时间与y也高度相关,从而在计算R’的时候,\(v/c vt_e\)出现了\(v^2\)。所以现在问题的关键,变成了为什么波前是\(R’(x-vt_r, y/gamma)\)而不是\((x-vt_r, y)\)
对R’,静止时方向为ccos,csin,运动时ccos变成了ccos-v导致变形,y方向变成了y/gamma
======
手动计算波前压缩:
在发射时刻t’,接收时刻t有:
c(t-t’)=R
对第二个波,时刻t’+dt’和t+dt:
\(c(t+dt-t’-dt’)=|R-vdt’|\)
\(=\sqrt{R^2-2v\cdot Rdt’+(vdt’)^2}\)
\(~R\sqrt{1-2n\cdot vdt’/R}\)
\(~R(1-n\cdot vdt’/R)\)
\(dt=dt’-(R/c-R(1-n\cdot vdt’/R)/c)\)
\(dt=dt’(1-n\cdot v/c)=dt’(1-vcos()/c)\)
注意到\(R(1-n\cdot vdt’)\)的大小实际上是\(R-vdt’\)在R上的投影大小:
\(|R-vdt’|=\sqrt{(R(1-n \cdot vdt’)^2+(v_\perp dt’)^2}\)
在dt’趋于0时,二阶小量\((v_\perp dt’)^2\)更快趋于0
伽利略变换和洛伦兹变换的区别,就在于这个二阶小量,它对应着vy/c,伽利略变换没有减去这个二阶小量,垂直方向仍然是y,洛伦兹变换减去了vy/c,变成了\(y/\gamma\)
推迟势的推导过程中的积分,使用了u=t-t’+R/c代替t’积分,实际上是从发射时间的积分过渡到了接收时间的积分,同时表明发射出的势能等于接收到的势能。
经过观察,我们会发现,光行差c-vcos()仅仅对应平行于R的分量,这个对应标量势,而矢量势部分\(n \times v\)=vsin()/c正好对应光源到R的垂线大小,也就是垂直于R的方向分量,这部分正对应磁场分量!!!
电荷运动,导致垂直电场变大,从而引起电场方向改变,而垂直部分变大的贡献完全来自于垂直于运动方向的磁场。而减去vsin()/c部分,实际上就是增加了磁场,而不是减去了磁场,但y方向几何长度变短。没有磁场时,就是伽利略变换。为了维持光速不变,必须要产生磁场。
我们也可以说,运动电荷通过切割自己的电力线,形成了时变分量\(\partial E/\partial t\),也就是磁场。
所以,相对论的本质是因为光速有限恒定,导致运动会累积垂直磁场分量,从而出现各种带gamma的变换。比如光线垂直发射速度为c,当增加相对水平速度v时,光线的垂直分量必须变成c/gamma,两者合成一个斜向的速度c。在推迟势变换中,观察者方向压缩为光行差式子,但垂直方向还会出现一个gamma,这个gamma来自磁场
所以,思路就是,在发射时间看波前,和在接收时间看波前,通过两者微分就可以得到两者变换关系,但两者对总电力线的积分也就是总能量是相等的,只是分布不同。由此可以得到静止观察者得到的新的等势面,等价于新的电场分布,与静止系电场分布比,多了个垂直的磁场。这个垂直的磁场在伽利略变换中不存在,因为伽利略变换没考虑延迟传播导致的拥挤效应从而导致光的传播角度变化导致垂直于运动方向的速度也会变化。
光行差计算时,使用\(dt/dt’=1-vcos()/c\),忽略了二阶小量,二阶时\(dt/dt’=1-vcos()/c+\frac{v^2sin^2()}{2c^2}\approx\sqrt{(x-vt)^2+y^2}\),一阶导数得到的光行差公式,是精确解,考虑二阶时会多出垂直分量,非精确解
推迟势的推导,使用了在某个瞬时时刻,势能是总电荷的体现,于是对瞬时时间t积分,即得到电荷。利用了发射时刻的电荷等于接收时刻都电荷,而积分时通过将dt’替换为dt,自然的得到了dt’/dt在分母:
\(\int \frac{1}{f(t’)}dt’=\int \frac{1}{f(t’)} dt\frac{dt’}{dt}=\frac{1}{f(t’)dt/dt’}\)
余弦定理,\(a^2=b^2+c^2-2bccos()=(b-ccos())^2+(csin())^2\), 所以:
\(R1^2/\Delta t=(c-vcos)^2+(vsin)^2=(ccos-v)^2+(csin)^2=(c-v)^2+2cv(1-cos)\)
远场下vsin忽略,得到c-vcos
\(R’=\sqrt{(x-vt)^2+(y/\gamma)^2}\)
标量势\(\phi=k\frac{1}{R’}\)
矢量势\(A=\frac{\mathbf{v}}{c^2}\phi\)
\(\frac{\partial R’}{\partial t}=-vcos(\theta’)\)
\(\frac{\partial A}{\partial t}=k\frac{v^2cos(\theta’)}{c^2R’^2}\hat{x}=k\frac{v^2}{c^2R’^3}(x-vt,0,0)\)
\(\Delta R’=\frac{1}{R’}(x-vt,\frac{y}{\gamma^2})\)
\(\nabla \phi=-k \frac{1}{R’^3}(x-vt,\frac{y}{\gamma^2})\)
\(E=-\nabla \phi-\frac{\partial A}{\partial t}=k \frac{1}{\gamma^2 R’^3}(x-vt,y)\)
\(B=\nabla \times A=k \frac{v}{c^2R'3}(0,-\frac{z}{\gamma^2},\frac{y}{\gamma^2})\)
\(\nabla \times (\mathbf{v} R’) = \frac{v}{\gamma^2 R’} (0, z, -y)\)
\(\mathbf{B} = -\frac{q}{4\pi\epsilon_0 c^2 R’^2}\nabla \times (\mathbf{v} R’)\)
\(\mathbf{B} = \frac{\mu_0}{4\pi} \frac{q \gamma (1 - \beta^2)\mathbf{v} \times \mathbf{R}}{[R^2 - (\mathbf{R} \times \mathbf{v}/c)^2]^{3/2}}\)
\(\frac{\mathbf{v} R’}{c} = \mathbf{v}(t-t’) \left(1 - \frac{v}{c}\cos\theta\right)\)
\(\mathbf{B} \propto \frac{\mathbf{v} \times \mathbf{R}}{R^3}=>vRsin()/R^3=vsin()/R^2\)
洛伦兹坐标变换得到的电场:
\(E’=-k \frac{1}{\gamma^2 R’^3}(x-vt,\frac{y}{\gamma})\)
\(E^2-(cB)^2=E’^2\)
标量势正比于1/R’,所以标量势的梯度正比于R’的梯度,R’仅代表标量势,而矢量势对t求导,和标量势的梯度合并后才是电场的方向,指向t时刻电荷到观测者的方向,也就是伽利略变换方向。也就是坐标变换是剔除了时变部分也就是磁场部分。只关注了光行差,也就是时间比
所以,R’的半径方向就是坐标变换的方向,R’是标量势的分布,R’的梯度,就是标量势的梯度,R’的时间导数,对应矢量势的时间导数。
从R1到R’,从E到E’,说明,洛伦兹变换等于伽利略变换减去磁场。
那么问题是,磁场到底是什么,它是如何储存和转化能量,从而使光线偏转方向从伽利略变换到洛伦兹变换的。磁场是对\(v(t-t’)(1-\frac{v}{c}cos(\theta)\)求旋度。显然光线不仅仅是简单的向上偏折方向
由于v的存在,y方向最大速度应该为\(c/\gamma\),所以\(csin(\theta’)/\gamma\)是合理的
电磁场能量密度:
\(u = \frac{\varepsilon_0}{2} E^2 + \frac{1}{2\mu_0} B^2 = \frac{\varepsilon_0}{2} E’^2 + \frac{1}{\mu_0} B^2\)
磁场就是电磁场的动能部分,静电场E’,在获得动能B后,合成了E。其中\(B=\gamma v \times E’/c^2\)
\(\mathbf{v} \times \mathbf{R}’ = \left( 0, \ v \cdot \frac{z}{\gamma}, \ -v \cdot \frac{y}{\gamma} \right)\)
二维:
\(\gamma (\mathbf{v} \times \mathbf{R}’) = v y\)
对应光源到R的垂线vy/c部分
这说明洛伦兹纯坐标变换对应R’=sqrt{(x-vt)^2+y^2/gamma^2},或对应R dt/dt’=R’,也就是只考虑了光行差部分,没有考虑垂直于光线的分量vy/c,也就是没有考虑磁场部分
也就是,观察者只关注不同光线之间的时间差,也就是同时性只体现的不同光线的时间差里,没有体现在电场强度里
\(\partial B/\partial t=\nabla \times (\partial A/\partial t) =( 0, \partial/\partial z (\partial A/\partial t), - \partial/\partial y (\partial A/\partial t) )\)
磁场在运动方向不随时间变化,\(\partial A/\partial t\)是磁场变化产生的感应电场
\(B = ∇ × A ≈ ( 0, ∂A_x/∂z, -∂A_x/∂y )\)
\(B_y = - (v / c²) E_z\)
\(B_z = (v/ c²) E_y\)
\(E_y ≈ - (c² / v) B_z\)
\(E_z ≈ (c² / v) B_y\)
磁场源于电流密度,源于电磁场动量。总电场与磁场的关系,就是电磁场总能量与动量的关系,动量等于能量的时间变化,对应牛顿第二定律,
F = dp/dt= -∇V
v = ∂E/∂p
\( p_x = \gamma m v= \frac{v}{c^2} E\)
\(v = c^2 \frac{p_x}{E}\)
==========
\(Rdt/dt’\)可以得到\(R’=(x-vt,y/\gamma,z/\gamma)\),对应洛伦兹坐标变换
光源在t时刻的即时位置\(R_1=(x-vt,y,z)\),
\(Rdt/dt’\)不等于\(R_1\),是因为t趋于t’时,决定大小和方向的是一阶导数,从\(R_1\)到R’丢掉了二阶导数,
\(\partial A /\partial t=(\frac{v^2}{c^2}(x-vt),0,0)\),使得R’或\(\nabla \phi\)变为\(\frac{1}{\gamma^2}(x-vt,y,z)\),对应总电场E
\(\nabla \phi\)扣掉了\(\partial A/\partial t\)也就是\(\frac{v^2}{c^2}(x-vt)\)后,就变成了总电场对应电荷瞬时位置,其中包含了磁场,如果扣掉磁场,就成了洛伦兹坐标变换后的电场等价于静电场
\((x-vt,y,z)^2=(x-vt,y/\gamma,z/\gamma)^2+(\frac{v}{c}(0,-z,y))^2\)
瞬时位置的电场=推迟方向的变换+磁场
\(\frac{dt}{dt’}\),对应的是沿光轴的纵向运动信息,它只依赖于速度在视线方向的投影 \(\mathbf{n} \cdot \mathbf{v}=vcos(\theta)\),它不包含速度的横向分量信息,是一个标量,只能改变场的大小,不能改变方向或产生新的方向性,用于处理时序和强度修正,负责:多普勒效应、时间膨胀
磁场是一个垂直于光轴的矢量,表示横向运动信息,方向是\(\mathbf{n} \times \mathbf{v}=vsin(\theta)\),用于处理几何和方向修正,处理速度的横向分量、场的空间变化率,磁场是运动电荷对电场线横向拖曳所产生的剪切涡旋场
两者是正交的:
\((\mathbf{n} \cdot \mathbf{v})^2 + |\mathbf{n} \times \mathbf{v}|^2 = v^2\)
从\(R-R_1\),也就是从(x-vt’,y)到(x-vt,y), 然后再减去\(\frac{v}{c}y\),因为x方向仍然是(x-vt),所以减去的是y方向的,y变成了\(y/\gamma\),但几何上如何构造?\(y^2-(vy/c)^2=(y/\gamma)^2\)
磁场的时间导数等于电场的旋度,说明电场的提供旋度的部分,来自产生磁场的矢量势的时间导数,
\(\nabla \times (-\nabla \phi)=0\),
\(\nabla \times \mathbf{E} = -\nabla \times \left(\frac{\partial\mathbf{A}}{\partial t}\right) = -\frac{\partial}{\partial t}(\nabla \times \mathbf{A}) = -\frac{\partial\mathbf{B}}{\partial t}\)
\(-\nabla \phi = \frac{q}{4\pi\epsilon_0} \frac{(x-vt, y/\gamma^2, z/\gamma^2)}{[ (x-vt)^2 + (y/\gamma)^2 + (z/\gamma)^2 ]^{3/2}}\)
\(-\frac{\partial \mathbf{A}}{\partial t} = -\frac{\partial}{\partial t} \left( \frac{v}{c^2} \phi \hat{\mathbf{x}} \right) = -\frac{v}{c^2} \frac{\partial \phi}{\partial t} \hat{\mathbf{x}}\)
\(E = \frac{q}{4\pi\epsilon_0} \frac{((x-vt)/\gamma^2, y/\gamma^2, z/\gamma^2)}{[ (x-vt)^2 + (y/\gamma)^2 + (z/\gamma)^2 ]^{3/2}}\)
\(\mathbf{B} = \frac{v}{c^2} \left( -\frac{\partial \phi}{\partial y} \hat{\mathbf{z}} + \frac{\partial \phi}{\partial z} \hat{\mathbf{y}} \right)\)
======
固定时间t’:
\(\frac{\partial }{\partial x}(R(1-vcos(\theta)/c))=\cos\theta-\frac{v}{c}=\frac{x-vt}{R}\),
\(\frac{\partial }{\partial y}(R(1-vcos(\theta)/c))=\sin\theta=\frac{y}{R}\),
\((\frac{\partial }{\partial x}(R(1-vcos(\theta)/c)))^2 + (\frac{\partial }{\partial y}(R(1-vcos(\theta)/c)))^2 = \left(1 - \frac{v}{c} \cos\theta \right)^2 + \left( \frac{v}{c} \sin\theta \right)^2\),
对应伽利略变换位置\(R^2_1=(x-vt)^2+y^2=R’^2 + (vy/c)^2\)
\(\frac{\partial R}{\partial x}=\cos\theta=\frac{x-vt’}{R}\),
\(\frac{\partial R}{\partial y}=\sin\theta=\frac{y}{R}\),
\(\frac{\partial}{\partial x} \left( 1 - \frac{v \cos\theta}{c} \right) = \frac{v \sin^2\theta}{cR}\)
\(\frac{\partial}{\partial y} \left( 1 - \frac{v \cos\theta}{c} \right) = \frac{v \cos\theta \sin\theta}{c R}\)
固定时间t(t’的完整导数):
\(\frac{\partial}{\partial x} ( R (1 - v \cos\theta/c )) = \frac{\cos\theta - v/c}{1 - v \cos\theta/c}\)
\(\frac{\partial}{\partial y} ( R (1 - v \cos\theta/c )) =\frac{\sin\theta}{\gamma^2(1 - (v \cos\theta)/c)}\)
\(\frac{\partial R}{\partial x} = \frac{\cos\theta}{1 - v \cos\theta/c}\)
\(\frac{\partial R}{\partial y} =\frac{\sin\theta}{1 - (v \cos\theta)/c}\)
\(\frac{\partial}{\partial x} \left( 1 - \frac{v \cos\theta}{c} \right) = \frac{v \sin^2\theta}{cR(1-v\cos\theta/c)}\)
\(\frac{\partial}{\partial y} \left( 1 - \frac{v \cos\theta}{c} \right) = \frac{v \cos\theta \sin\theta}{c R}\)
\(\frac{\partial}{\partial y} \left[ 1 - \frac{v}{c} \cos\theta \right] = \frac{v \sin\theta \left( \cos\theta - \frac{v}{c} \right) }{c R \left( 1 - \frac{v}{c} \cos\theta \right)}\)
\(\frac{\partial t’}{\partial y}=\frac{\sin\theta}{c(1-v\cos\theta/c}\)
\(\frac{\partial R}{\partial y}=-c\frac{\partial (t-t’)}{\partial y}=-c\frac{\partial t’}{\partial y}\), 所以:
\(\frac{\partial}{\partial y} ( R(1 - \frac{v \cos\theta}{c}) ) \)
\(= \frac{\partial}{\partial y} ( R - \frac{v (x-vt’)}{c} )\)
\(=\frac{\partial}{\partial y} ( R + \frac{v^2}{c}t’ )\)
\(=\frac{\partial}{\partial y} ( R - \frac{v^2}{c^2}(t-t’) )\)
\(=\frac{\partial}{\partial y} ( R/\gamma^2)\)
即:\(\partial R’/\partial y=\frac{1}{\gamma^2}\partial R/\partial y\)
\(\frac{\partial}{\partial y} (x-vt’)\)
\(= \frac{\partial}{\partial y} ( (-vt’) )\)
\(= \frac{\partial}{\partial y} ( (vt-vt’) )\)
\(=\frac{\partial}{\partial y} ( \frac{v}{c}R )\)
\(=\frac{v}{c}\frac{\partial R}{\partial y} \)
可见,在t固定时,y的变化显著影响R的变化从而影响t’的变化
梯度与切线方向:
R的梯度:
\(\nabla R=(\cos\theta,\sin\theta)\),
切线方向:\((-\sin\theta,\cos\theta)\)
\(R’ = \sqrt{(x - vt)^2 + \frac{y^2}{\gamma^2}}\)的梯度:
\(\nabla R’ = ( \frac{x - vt}{R’},\ \frac{y}{\gamma^2 R’} )=(\cos\theta’,\sin\theta’/\gamma)\),对应\(-\nabla \phi\)
切线方向:\(( -\frac{y}{\gamma^2 R’},\ \frac{x - vt}{R’})\), y方向对应磁场部分
x’,y’值由旋转产生:
也就是由\(x_0=R’cos\theta, y_0=R’sin\theta\),变成了\(x’=R’cos\theta’=x_0-vt, y’=R’sin\theta=y_0/\gamma\)
=======
x方向:
\(c\cos\theta(t-t’)=x-vt’\),
所以:
\(\frac{dt}{dt’}=\frac{c\cos\theta-v}{c\cos\theta}\)
光速:
\(u’_x=c\cos\theta’=\frac{c\cos\theta-v}{dt}dt’=(c\cos\theta-v)\frac{dt’}{dt}=\frac{c\cos\theta-v}{1-v\cos\theta/c}\)
y方向:
为了光速不变,y方向光速分量为:
\(u’_y=c\sin\theta’=\frac{c\sin\theta}{\gamma(1-v\cos\theta/c)}\)
实际上是光的方向发生变化,在x方向偏移多出了速度v,而不是什么光速不变。接收者的时间发生了变化,由光源的t’到接收者的t,导致光速分量不同,从而光的方向发生了变化。y方向的光速被迫被动变化。光为了获取平移速度v,被迫降低角度,使得y方向光速分量变小。
这个多出的速度v,是系统的整体移动,电荷的移动v加上电场的移动v,所以电场仍然以电荷为核心,而电场的整体移动,是以增加了磁场导致电场方向改变来实现的,或者说是以前加速的时候,对电场做功让电场有了动能,动能即磁场。
=====
即:在实验室静止坐标系内观察,光相对于光源的速度,x方向为\(c\cos\theta-v\), 考虑时间因素,光源内坐标系光的速度应该是\(\frac{c\cos\theta-v}{dt}dt’\)。
为什么考虑时间因素?因为各个坐标系都认为自己坐标系内光速为c,而这个光速实际上是自有坐标系内的光速,也就是作为静止坐标系发射光线测到的光速,可以认为是自己坐标系内能量振动的传播速度。但为了让外来光线也保持光速不变,那就需要使用相对距离除以接收时间,才能使光速不变。而进入本坐标系的外来光,可能已经完全不同了,但相对距离和接收时间间隔仍然没变,所以用这两个量测出的光速仍然是不变的。同时这两个值,可以计算出发射者的光速情况。其中还涉及光的频率和相位。
======
为什么要以接收时间为准?
我们还是以一维为例,
一维时,有 \(c(t-t’)=x-vt’\),
光相对于光源的速度为c-v, 光走的时间为\(\Delta t’=t-t’\),
光走的相对距离为 \((c-v)\Delta t’\),
但在光源内的坐标系的人看来,自己坐标系内光速始终为c,光走了\(t_1\)时间,距离就是\(c t_1\),
于是有:\((c-v)\Delta t’=c t_1\)
即:\(\frac{相对速度}{光速}=\frac{t_1}{\Delta t’}\)
而在一维情况下,相对光速除以光速,正好是接收时间差除以发射时间差1-v/c,
这是因为,在时刻t,光源再发射一束光,那么这束光走的距离就是\(c t_2=(c-v)\Delta t’=c t_1\)
第一束光在时刻t收到,然后经过\(t_2\)时刻,第二束光收到,所以接收时间差就是\(t_2\),
也就是接收时间差,即光源坐标内,用光速c测量t时刻距离需要的时间
那么在三维情况下,我们相信也是如此,x方向上:
\(\frac{c\cos\theta-v}{c\cos(theta’)}=\frac{dt}{dt’}\)
即:\(c\cos(theta’)=\frac{(c\cos\theta-v)}{1-v\cos(\theta)/c}\)
那么为什么不是\(\frac{c\cos\theta-v}{c\cos(theta)}=\frac{dt}{dt’}\)呢?
我们先看看\(\frac{c\cos\theta-v}{c\cos(theta)}\),
\(\frac{x-vt}{x-vt’}=\frac{x-vt’-v(t-t’)}{c-vt’}=\frac{R\cos\theta-vR/c}{R\cos\theta}=\frac{c\cos\theta-v}{c\cos(theta)}\)
可见其等于\(\frac{x-vt}{x-vt’}\)
但实际上,因为我们要固定观测点,所以不同时刻,光的倾斜角度是不同的,所以水平速度实际上发生了变化,不再是\(c\cos\theta\),光走的距离是x-vt,但时间已经不是x-vt和x-vt’的对应关系\(\frac{c\cos\theta-v}{c\cos(theta)}\)了,而是变成了\(\frac{c\cos\theta-v}{c-v\cos(theta)}\)。
至于为什么y轴变成了\(y/\gamma\),这是光路倾斜计算得到的结果,就和光在运动坐标系内垂直发射,在静止坐标系内为了获得水平速度v,垂直方向速度分量必须变成\(c/\gamma\),无须再探究其几何形式,其本质是能量和动量守恒的要求,系统内的光获得了一个水平方向的(角)动量。