参考：
我们得到不同参考下下，光速不变的原因在于转换使用了\(\frac{dt}{dt’}=\frac{R’}{R}\)的原因，
现在我们把问题重述一遍。
在\(\hat{x}\)轴方向上，运动光源沿着\(\hat{x}\)轴从t’发射光子，到观察点x, 经历了时间t，
此时有两个关系式：
\(x-vt’=c(t-t’)\)
可以计算出 \(\frac{dt}{dt’}=\frac{c-v}{c}\)
也可以手工计算：
光源在\(t’_1\)和\(t’_2\)时刻发射两个光子，观察点\(x\)在\(t_1\)和\(t_2\)时刻接收到，此时：
\(x-vt’_1 =c(t_1-t’_1)\)
\(x-vt’_2 =c(t_2-t’_2)\)
得：
\(v(t’_2-t’_1)=c(t’_2-t’_1)-c(t_2-t_1)\),
即：\(\frac{\Delta t}{\Delta t’}=\frac{c-v}{c}\)
所以，使用求导得到时间的间隔关系，是靠谱的。
也就是固定接收者接收到两个光子的时间间隔，和光源发射两个光子的时间间隔，比例是\(\frac{c-v}{c}\)，这就造成了固定坐标系和移动坐标系造成的时间问题。
而发射一个光子，在固定坐标系内看，走的距离是\(c(t-t’)\)，
在观察者看来，走的距离是\(c(t-t’)-v(t-t’)=(c-v)(t-t’)\)，
可见两者的距离比例与两者的时间比例相同，所以光速不变。
也可以用前面的两个光子来计算，
在固定坐标系，两个光子距离为\(ct’_2-ct’_1)\)，时间间隔为\(t’_2-t’_1\)，光速为c
在运动坐标系看来，两个光子距离为：
\(c(t’_2-t’_1)-v(t’_2-t’_1)=(c-v)(t’_2-t’_1)\)
\(=(c-v)(t_2-t_1)\frac{c}{c-v}=c(t_2-t_1)\),
可见如果两个光子的间隔计时采用观察者收到时的\(t_2-t_1\)，而不是光源发射时的\(t’_2-t’_1\)，则光速仍然为c
我们改用前面得到的\(\frac{dt}{dt’}\)来计算，
前面我们得到：
\(\frac{dt}{dt’}=1-\frac{v}{c}\frac{x-vt’}{R}\)
x轴上，有y=z=0, R=x-vt’，所以：
\(\frac{dt}{dt’}=1-\frac{v}{c}\)
本质就是：
在静止坐标系看来，光走的距离为光源时刻t’到接收时间t走的距离，也就是\(x-vt’=c(t-t’)\), 时间为\(dt’=t-t’=\frac{x-vt’}{c}\)
在接收者看来，光走的距离为接收时刻t时，接收点到光源的距离：\((x-vt)=(c-v)(t-t’)\)，时间为\(dt=\frac{c-v}{c}(t-t’)=\frac{x-vt}{c}\)
即：
\(\frac{x-vt’}{dt’}=\frac{x-vt}{dt} =c\)
且：
\(dt’-dt=t-t’-\frac{c-v}{c}(t-t’)=\frac{v}{c}(t-t’)=\frac{v}{c}\frac{dx}{c}=\frac{v dx}{c^2}\)
这就是洛伦兹变换里\(\frac{vx}{c^2}\)的来源。
实时上，大多数情况下，我们使用下列变换就够用了：
\(x’ =x+vt \)
\(t’ =t+\frac{vx}{c^2}\)
比如电磁波的波动方程
============
再看y方向：
运动坐标的\(\hat{y’}\)轴上，有\(x’=0,x=vt，z=0\)，
所以 \(R=\sqrt{(vt-vt’)^2+y^2}\)
前面我们计算过：
\(t’ = \frac{c^2 t - x v - c\sqrt{(x - v t)^2 + (1 - v^2/c^2)(y^2 + z^2)}}{c^2 - v^2}\)
将\(x=vt,z=0\)代入t’，则：
\(t’=t-\frac{y}{c\sqrt{1-v^2/c^2}}=t-\frac{\gamma y}{c}\)
代入R，可得：
\(R=\gamma y\)
代入\(\frac{dt}{dt’}\)，可得：
\(\frac{dt}{dt’}=1-\frac{v}{c}\frac{vt-vt’}{\gamma y}=1-\frac{v^2}{c^2}=\frac{1}{\gamma^2} \)
那么观察者在收到光子后到光源的距离y’就是：
\(y’=R’=R\frac{dt}{dt’}=\gamma y \frac{1}{\gamma^2} =\frac{y}{\gamma}\)
在\(\hat{y’}\)轴上，有：
\( \frac{R’}{dt}=\frac{R}{dt’}=c \)
此时运动坐标系上的\(\hat{y’}\)轴上光速不变，也就是，只要此时在\(\hat{y’}\)轴上的值为\(y/\gamma\)，则两个坐标系都满足光速不变。
至于\(\hat{y}\)轴上的距离\(y’\)为什么是\(y/\gamma\)而不是\(y\)，可以如下理解：
在光源处于静止坐标系原点时，发射一个光子，沿着光源的\(\hat{y’}\)轴前进，那么沿着光源的\(\hat{y’}\)轴前进的话，在静止坐标系看来实际上是斜着走的，斜率为\(v/c\),如下图：
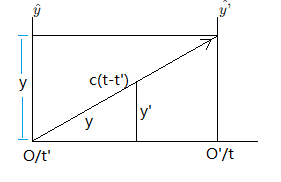
在光沿着\(\hat{y’}\)轴前进时，光走的距离为\(R=c(t-t’)\)，在\(\hat{y}\)轴上的投影值为\(y\)，
而如果在O坐标原点同时发射两个光子，一个沿着\(\hat{y}\)轴，一个沿着\(\hat{y’}\)轴前进，则：
第二个光子走的距离为\(R=y=c(t-t’)\)，此时在\(\hat{y’}\)轴上的投影就是\(y/\gamma\)
也就是说，虽然从时间t’到t，光走的距离是c(t-t’)，但我们要保证光在两个坐标系内走的距离也相同，如果在\(\hat{y}\)上走的距离为y，那么必须也要保证任意方向的距离也是y才能保证事件的同时性，也就是要在\(c((t-t’)\)上截取\(y=c(t-t’)/\gamma\)，而\(c(t-t’)/\gamma\)在O’坐标系内的\(\hat{y’}\)方向的投影是\(c(t-t’)/\gamma^2=y/\gamma\)
也就是，光沿着光源的y方向前进的话，发射光子的时间差和接收光子的时间差的比值前面算出来是\(\gamma^2\)，同时光子在光源的y方向走的距离映射为\(R’=y/\gamma=c(t-t’)/\gamma^2=R/\gamma^2\)，所以体现出来的就是光速不变。
那么在洛伦兹变换中，使用了相同的y，这就导致了移动坐标系的y值要扩大\(\gamma\)倍，从而x方向和时间也扩大了\(\gamma\)倍(由(\(x-vt,y/\gamma,z/\gamma\))到(\(\gamma(x-vt),y,z)\))，这样光速仍然是不变的，方便了坐标变换，而推迟势中采用了测量相同的x位置，这导致了在其他的坐标变换中比如电势和电场的坐标变换中失真（电场的坐标变换，x方向不变，y方向(密度)扩大\(\gamma\)倍)，也就是洛伦兹变换采用了y不变，粒子的性质没有改变，比如电荷的静电场变换到移动坐标系，并不包含磁场，和原来的电场性质完全相同。
这也能解释为什么对一个电荷加速，不能加速到光速，因为此时\(y/\gamma\)将趋于0，也就是电力线的密度将无限大，能量(磁场)将趋于无限大。
问题：如果观测点相对于光源位置不变，该怎么计算？可以把当前光源作为静止坐标系，此时的推迟势怎么计算？