参考:
假设一个光源,以匀速\(v\)沿着x轴运动,
在空间一个观察点,相对于静止坐标系坐标\((x,y,z)\)
也就是此时静止坐标系内,\(A\)点在\(\hat{x}\),\(\hat{y}\)轴的的比例关系为\(x/y\)
光源在\(t_0\)时刻发射一个光子,观察点\(A\)在时间\(t\)时收到这个光子,
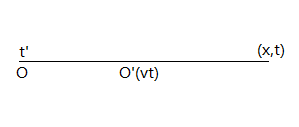
假设观察点\(A\)在\(x\)轴上,那么\(A\)收到光子时的观察点到光源的距离\(x’\)为:
\(x’=x-vt\),
光走的时间距离为:
\(x-vt’=c(t-t’)\)
图例如下:
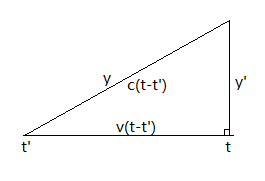
假设观察点\(A\)在y轴上,那么\(A\)收到光源发射的光子的时候,
光子相对于静止坐标系走了距离\(y\)的时候,则在\(y’\)中实际走的距离为:
\(y’=y/\gamma\),
此时光源发射光子,必须是斜向发射,以角度\(v/c\)的方向发射,才能始终保证光子在光源的\(\hat{y}\)轴上滑动
图例如下:
所以,在静止坐标系里的坐标\(ct=(x,y,z)\),运动坐标系里就变成了:
\(ct’=(x-vt,y/\gamma,z/\gamma)\)
这就是推迟势从\(R(ct,x,y,z)\)到\(R’(ct’,x-vt,y/\gamma,z/\gamma)\)的由来,
也就是在运动坐标系内,在同一个\(t’\)内,\(\hat{x}\), \(\hat{y}\)轴的比例关系变成了\((x-vt)/(y/\gamma)\)
那么,怎么从这点推导出洛伦兹变换?
在狭义相对论中,有形式:
\((ct)^2 =x^2+y^2+z^2\), \((ct’)^2 =x’^2+y’^2+z’^2\),
在光源沿着x轴运动时,两个坐标的y,z值是不变的,
这就需要\(\hat{y}\)轴由\(y/\gamma\)扩大到\(y\), 则对应的\(x’\)也要扩大\(\gamma\)倍,由\(x-vt\)扩大到\(\gamma(x-vt)\),同时时间也要扩大\(\gamma\)倍,此时\(R’\)变成了:
\(R’(ct’, \gamma(x-vt), y, z)\),
也就是计算的时候,认为发射的光子的位置,不是接收到光子时光源的真实位置\(x’=x-vt\),而是\(x’=\gamma(x-vt)\),这个并非真实观察者的结果,而是为了计算转换方便,只要能保持光速不变就行。
变换的时候,由于使用的是\(\frac{dt}{dt’}=\frac{R’}{R}\),即\(\frac{R’}{dt}=\frac{R}{dt’}=c\),\(dt\)对应运动坐标系,所以在不同坐标系内,这种变换都是光速,即使在洛伦兹变换中运动坐标系内时间和距离同时扩大了\(\gamma\)倍。
在电磁势坐标变换中,遵循 \(R(ct,x,y,z)\)到\(R’(ct’,x-vt,y/\gamma,z/\gamma)\)的变换,对R’求梯度,则可得出y,z方向电场变大\(\gamma\)倍
在静电场\(E_0\)的坐标变换中,可以使用洛伦兹变换变成\(E’_0\),并加上带\(\gamma\)的磁场B,则总电场E符合:
\(E^2 =E’_0^2+(cB)^2=E’_0^2(cos^2(\theta)+\gamma^2sin^2(\theta))\)
=========================================
通过对比发现,推迟势和狭义相对论在移动坐标系中的光线路径是相同的,
推迟势的路径公式为\(R’=\sqrt{(x-vt)^2+(y^2+z^2)/\gamma^2}\)
狭义相对论的路径公式为\(R’=\sqrt{\gamma^2(x-vt)^2+y^2+z^2}\)
它们的斜率是相同的,一个是\((y/\gamma)/(x-vt)\), 一个是\(y/(\gamma(x-vt)\)
只是它们采用的观察模式不同,
推迟势观察的是相同的x的情况,狭义相对论观察采用的是使用相同的y
如下图:
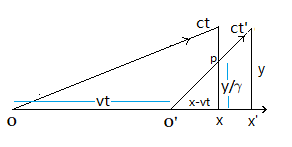
狭义相对论认为,坐标变换,在y方向上没有变化,在x方向上才有变化,计算的是相同的y情况下的变换(图中\(\triangle Ox-ct\)和\(\triangle O"x-ct\)),O’‘到x的距离为\(\gamma(x-vt)\),也就是\(\triangle O’xp\)的\(y/\gamma\)增大到\(y\)后,对应的\(x-vt\)会增加到\(\gamma(x-vt)\),变成了\(\triangle O"x-ct\),也就是接收者认为运动坐标系发射光子的位置为为O’’,对应的x的相对于O’‘的位置\(x’=\gamma(x-vt)\),这导致了时间膨胀(距离从O’P到ct",接收时间差\(dt\)增加到了\(\gamma dt\))。
推迟势的计算认为,电磁波在x方向上密度没有变化,在y方向上有挤压,也就是在不同坐标系,相同x的时候的密度情况(图中\(\triangle Ox-ct\)和\(\triangle O’xp\))。如果在相同的y的位置测量,则可能测到移动电荷的电场只在x方向增强,y方向相同,磁场也小了\(\gamma\)倍。
类似下图,
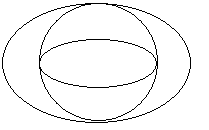
圆球内的小椭圆,x方向没变,y方向压缩
圆球外的大椭圆,y方向没变,x方向变大
狭义相对论使用了一个虚假的O’坐标位置(vt’+x-x’),使用了ct"这条线,而电磁场变换则使用了t时刻的真实的O’的位置(vt’+v(t-t’)=vt),使用了R’这条线,所以最终导致了两者的不同,导致了电磁场变换和狭义相对论变换的不同,同理相对论的能量动量关系式也是用了R’这条线。
推迟势下:
\(\frac{dt}{dt’} =1-\frac{v}{c}\frac{x-vt’}{R}\)
狭义相对论下的时间关系变为:
\(\frac{\gamma dt}{dt’} =\gamma(1-\frac{v}{c}\frac{x-vt’}{R})\)
接收时间\(dt\)拉长了\(\gamma\)倍,
在x轴上,\(y=z=0\),\(R=x-vt’\)有:
\(\frac{\gamma dt}{dt’}=\gamma(1-\frac{v}{c})\)
若\(dt’=t-t’=\frac{x-vt’}{c}\),有:
\(\gamma dt=\gamma(1-\frac{v}{c})(t-t’)=\gamma(dt-\frac{v dx}{c^2})=\frac{\gamma(x-vt)}{c}\)
在y轴上,x=0,有:
\(\frac{\gamma dt}{dt’}=\frac{1}{\gamma}\)
所以在一维的情况下,用x对齐的方法,不能得到洛伦兹变换
推迟势下:
\(\frac{dt}{dt’}=1-\frac{v}{c}\)
\(\frac{dt’}{dt}=\gamma^2 (1+\frac{v}{c})\)
\(\Delta x=\Delta x’+v \Delta t\)
\(\Delta t’=\Delta t+\frac{v \Delta x’}{c^2}\)
\(y’=\frac{y}{\gamma}\)
将dt扩大\(\gamma\)倍后,有:
\(\frac{\gamma dt}{dt’}=\gamma(1-\frac{v}{c})\)
\(\frac{dt’}{\gamma dt}=\gamma (1+\frac{v}{c})\)
\(\Delta x=\gamma(\Delta x’+v \Delta t)\)
\(\Delta t’=\gamma(\Delta t+\frac{v \Delta x’}{c^2})\)
\(y’=y\)
对\(\gamma R’\)路径,有:
\(\frac{dt’}{dt}=1+\gamma \frac{v}{c}\frac{x-vt}{R’}\)
令\(x’=\gamma(x-vt)\),
\(c \Delta t_2=\gamma R’=\gamma R(1-\frac{v}{c}{x-vt’}{R}\)
\( =\gamma c (t-t’)(1-\frac{v}{c}{x-vt’}{c(c-t’)}\)
令t’=0,则:
\(\Delta t_2=\gamma (t-\frac{xv}{c^2})\)
就得到了洛伦兹变换:
\(x’=\gamma(x-vt)\),
\(t’=\gamma (t-\frac{xv}{c^2})\)
过程:
移动光源发射光子,满足 \(c(t-t’)=R=\sqrt{(x-vt’)^2+y^2+z^2}\)
有:\(\frac{dt}{dt’}=1-\frac{v}{c}\),说明在固定的观察点,接收时间间隔和发射时间间隔不同
那么在光源的坐标系内,我们认为接收时间应该和发射时间相同,所以光源坐标系内,我们认为发射时间间隔是\(dt\),
所以当静止坐标系内,发射时间间隔为\(dt’=t-t’\)时,光源认为自己的发射时间间隔为\(dt=\frac{dt}{dt’}(t-t’)=\frac{dt}{dt’}\frac{R}{c}=\frac{R’}{c}\)
但\(R’=\sqrt{(x-vt)^2+(y^2+z^2)/\gamma^2}\),y的值缩小了\(\gamma\)倍,所以需要将R’扩大\(\gamma\)倍,有\(\gamma R’=\sqrt{\gamma^2(x-vt)^2+y^2+z^2}\),把发射光的位置,从位置x=vt的原点位置移到了\(x=x-\gamma(x-vt)\)
这正是洛伦兹变换的位置,是将接收时间dt扩大了\(\gamma\)倍
========================
根据关系式:
\(R=\gamma (\frac{\gamma (x - v t)v}{c} + \gamma R’)\)
\(\gamma R’=\gamma(R-\frac{(x-vt’)v}{c})\)
令\(R"=\gamma R’\),\(x’=\gamma(x-vt)\),\(x=x-vt’\)则有:
\(R=\gamma (R"+\frac{v x’}{c})=\sqrt{x^2+y^2+z^2}\)
\(R"=\gamma(R-\frac{v x}{c})=\sqrt{x’^2+y^2+z^2})\)
这个就是三维形式的洛伦兹变换,两边除以c,就有:
\((t-t’)=\gamma (\frac{R"}{c}+\frac{v x’}{c^2})\)
\(\frac{R"}{c}=\gamma((t-t’)-\frac{v x}{c^2})\)
其中\(\frac{R"}{c}=\gamma \frac{dt}{dt’}(t-t’)\)
这个就是洛伦兹变换的时间变换部分
=========== 再次补充 ===============
我们有个疑问,为什么在移动坐标系内,光线方向是R’,按说在光源自己的坐标系内,应该有\(\frac{dt}{dt’}=1\), 也就是发射时间间隔等于接收时间间隔,
我们发现,
\(\frac{dt}{dt’}=1-\frac{v}{c}\frac{(x-vt’)}{R}=1-\frac{v}{c}cos(\theta)\),这个式子说明由于光源运动,光在R方向上的速度,减少了\(vcos(\theta)\),也就是v在R方向上的投影,这是接收时间间隔不等于发射时间间隔的原因。
由上面的关系式,可以得到:
\(\frac{dt}{(1-\frac{v}{c}cos(\theta))dt’}=1\)
那么,在光源的坐标系内,我们能确切的得到接收时间t的间隔,但对发射时间间隔t’是不知道的,他们只知道自己的发射时间间隔,设为t", 则在光源的坐标系内,因为发射时间间隔等于接收时间间隔,会有:
\(\frac{dt}{dt"}=1\)
于是就有:
\(dt"=(1-\frac{v}{c}cos(\theta)) dt’\)
那么,我们假设在光源坐标系内,从x’处发射光线到观察点,观察点坐标为(x’,y,z),时间间隔为\(\Delta t"\),我们令:
\(\Delta t"=m dt"=m(1-\frac{v}{c}cos(\theta)) dt’=m(1-\frac{v}{c}cos(\theta))(t-t’)\),
则有:
\(c \Delta t" =\sqrt{x’^2+y^2+z^2}\)
即\(m c(t-t’)(1-\frac{v}{c}cos(\theta))=\sqrt{x’^2+y^2+z^2}\),
由于 \(R’=R\frac{dt}{dt’}=c(t-t’)(1-\frac{v}{c}cos(\theta))\),有:
\(mR’=\sqrt{x’^2+y^2+z^2}\),
即:\(m \sqrt{(x-vt)^2+(y^2+z^2)/\gamma^2}=\sqrt{x’^2+y^2+z^2}\),
两边\(x^2+y^2\)参数相等,可得:
\(m=\gamma\),
\(x’=\gamma(x-vt)\)
===== 总结:
在移动坐标系使用静止坐标系的时钟的情况下,有变换:
\(x=x’+vt’\)
\(t=t’+x’v/c^2\)
\(x’=\gamma^2(x-vt)\)
\(t’=\gamma^2(t-xv/c^2)\)
光在移动坐标系内观察到的路径:
\(R’=\sqrt{(x-vt)^2+(y^2+z^2)/\gamma^2}\)
适用于推迟势,电磁场,能量转换:横向压缩,纵向不变
在移动坐标系使用自己的时钟计时时,有:
\(x=\gamma(x’+vt’)\)
\(t=\gamma(t’+x’v/c^2)\)
\(x’=\gamma(x-vt)\)
\(t’=\gamma(t-xv/c^2)\)
光在移动坐标系内观察到的路径:
\(R’=\sqrt{(\gamma(x-vt))^2+y^2+z^2}\)
适用于坐标变换:纵向拉伸,横向不变
================再补充==
由\(\frac{dt}{dt’}=1-\frac{vcos(\theta)}{c}=\frac{R’}{R}\),
有:
\(\frac{R}{c}=\frac{R’}{c-vcos(\theta)}=t-t’\),
可见,在静止坐标系内观察,光相对于光源的相对速度为\(c-vcos(\theta)=c\frac{R’}{R}\),
在时间t时,相对于光源的距离为\((c-vcos(\theta))(t-t’)\)
\(x\)方向相对于光源位置为\(x-vt\),
那么光相对于光源的角度则是:
\(cos(\theta’)=\frac{x-vt}{(c-vcos(\theta))(t-t’)}=\frac{x-vt}{R’}\)
如果在经过时间\(\Delta t\),到达观察点时,有:
\(y^2+z^2=(((c-vcos(\theta)) \Delta t)sin(\theta’))^2=(c \frac{R’}{R} \Delta t)^2 (1-(\frac{x-vt}{R’}))^2\)
可得:
\(c \Delta t =\gamma R\)
于是有:
\(\Delta t=\gamma(t-t’)\),
可见,在静止坐标系看来,光相对于光源,以相对速度\(c-vcos(\theta)\),相对角度\(cos(\theta’)=\frac{x-vt}{R’}\),要想到达同一个观察点,需要多\(\gamma\)倍时间,
此时相对于光源的光路径为\((c-vcos(\theta))\gamma(t-t’)=\gamma R’\)。
而在光源的坐标系看来,要保持计算的光的速度为c,则必须以接收者的时钟t来计算时间,此时:
在发射时间差为\(\Delta t’=t-t’\)时,接收时间差为\(\Delta t=(1-\frac{v}{c}cos(\theta))(t-t’)=\frac{R’}{c}\)
所以有 \(\frac{R’}{\Delta t}=c\),
在移动坐标系看来,发射时间和接收时间应该是同步的,在不能确定远处光源的发射时间的时候,使用接收时间是靠谱的。
从R到R’,说明静止坐标系使用了发射时间来计算移动坐标系的长度,导致长度缩短,造成了尺缩效应。而从R’到\(\gamma R’\),使用了接收时间后,造成了时间膨胀。
================ 再补充 =
在R坐标系内:
\(c(t-t’)=R\), \(R=\sqrt{(x-vt’)^2+y^2+z^2}\)
\(\frac{dt}{dt’}=1-\frac{v(x-vt’)}{cR}\)
在R’坐标系内:
\(c(t_2-t’_2)=R’\), \(R’=\sqrt{(x-vt_2)^2+(y^2+z^2)/\gamma^2}\)
\(t = \frac{ c^2 t’ - x v + c \sqrt{ (x - v t’)^2 + \dfrac{y^2}{\gamma^4} } }{ c^2 - v^2 }\)
\(\frac{dt’_2}{dt_2}=1+\frac{v(x-vt_2)}{cR’}\)
\(\frac{dt}{dt’} = \gamma^2 \left( 1 - \frac{v}{c} \cdot \frac{x - v t’}{ \sqrt{ (x - v t’)^2 + \left( \dfrac{y}{\gamma^2} \right)^2 } } \right)\)
我们让两个坐标系的dt相等,也就是dt=dt_2,也就是在x-vt’和x-vt指向同一个x的时候,接收者的两个坐标的时间差相同,使用了相同的时钟
则 \( dt’_2=dt_2(1+\frac{v(x-vt)}{cR’})=dt(1+\frac{v(x-vt)}{cR’})\)
又因为 \(dt=dt’(1-\frac{v(x-vt’)}{cR})\),所以:
\(dt’_2=dt’(1+\frac{v(x-vt)}{cR’})(1-\frac{v(x-vt’)}{cR})\),
由\((1+\frac{v(x-vt)}{cR’})(1-\frac{v(x-vt’)}{cR})=\frac{1}{\gamma^2}\),有:
\(dt’_2=\frac{dt’}{\gamma^2}\)
如果在y,z相同时,则有:
\(dt_2=\gamma dt\), \(dt’_2=\frac{dt’}{\gamma}\)
前者明显代表时间膨胀,后者可能代表了长度收缩
也就是在\(\gamma R’\)路径内,接收端接收到光线,花的时间间隔是R路径接收端时间间隔的\(\gamma\)倍
如果使用相同的发射时间时钟,\(dt’_2=dt’\),
则\(dt_2=\frac{dt’_2}{1+\frac{v(x-vt)}{cR’}}=\frac{dt}{(1-\frac{v(x-vt’)}{cR})(1+\frac{v(x-vt)}{cR’})}=\gamma^2 dt\)
要想两个坐标系的y,z相同,则要\(dt’_2=dt’/\gamma\),与前面相同。
所以,只要满足\(dt’_2=dt’/\gamma\),\(dt_2=\gamma dt\),就可以满足x,y相同
且有:
\((\frac{dt}{dt’})_{_R}=\frac{1}{\gamma^2}(\frac{dt}{dt’})_{_R’}\)
============== 再分析为什么\(y’=y/\gamma\)
在R系中,有:
\(cos(\theta)=(x-vt’)/R\),
\(c_x=c cos(\theta)\), \(v_y=c sin(\theta)\),
则有\((t-t’) \sqrt{c_x^2+c_y^2} =R\),
那么对R’系:
\(R’=\sqrt{(x-vt)^2+y^2/\gamma^2}\),
\(cos(\theta’)=(x-vt)/R’\),
\(c_x’=c cos(\theta’)\), \(c_y’=c sin(\theta’)\),
经过推导,可得:
\(c_x’ = \frac{ c \cos\theta - v }{ 1 - \frac{v}{c} \cos\theta } \)
\(c_y’ = \frac{ c \sin\theta }{ \gamma \left(1 - \frac{v}{c} \cos\theta\right) }\)
但在R坐标系内,我们认为光相对于R’的速度应该是:
\(c_x’=c \cos\theta-v\), \(c_y’=c \sin\theta/\gamma\), 有:
\(c_x’^2+c_y^2 =(v-c \cos\theta)^2=\frac{R’}{(t-t’)}\)
即:
\(R’=(t-t’)\sqrt{(c cos\theta-v)^2+(\frac{c sin\theta}{\gamma})^2}\)
也就是,在R坐标系内看,光相对于R’坐标系,
\(c_x’=c cos\theta -v=c_x-v=\frac{x-vt}{t-t’}\)
\(c_y’ =\frac{y’}{t-t’}=\frac{c sin\theta}{\gamma}=\frac{c_y}{\gamma}=c \sin\theta’ \frac{dt}{dt’}\)
\(\Delta t=t-t’=\frac{R}{c}\)
\(\frac{x-vt’}{c_x}=\frac{x-vt’}{c cos\theta}=t-t’=\frac{R}{c}\)
\(\frac{x-vt}{c’_x}=\frac{x-vt}{c cos\theta-v}=t-t’=\frac{R}{c}\)
\(t’ = \frac{x - c \cos\theta \cdot t}{v - c \cos\theta} = \frac{c_x t-x}{c_x-v}=t\frac{c_x-x/t}{c’_x}\)
\(t’ = t- \frac{x - vt}{c \cos\theta - v}=t-\frac{x-vt}{c’_x}\)
\(x-vt=(t-t’)(c cos\theta-v)=c’_x(t-t’)\)
\(y’=c(t-t’) \sin\theta’ \frac{dt}{dt’}\)
在R’坐标系内看,光的速度分量是:
\(c_x’ = c \cos\theta’ =\frac{ c \cos\theta - v }{ 1 - \frac{v}{c} \cos\theta }= (c \cos\theta - v)\frac{dt’}{dt}\)
\(c_y’ = c \sin\theta’ =\frac{ c \sin\theta }{ \gamma \left(1 - \frac{v}{c} \cos\theta\right) }=\frac{ c \sin\theta }{ \gamma}\frac{dt’}{dt}\)
\(\Delta t=(t-t’)(1 - \frac{v}{c} \cos\theta)=\frac{R’}{c}\)
\(\frac{x-vt}{c’_x}=\frac{x-vt}{c cos\theta’}=\frac{R’}{c}\)
\(\gamma\)只是用来调整相同y时的参数,也是时间膨胀和长度收缩的原因,来自:
\(\cos \theta’ = \frac{x-vt}{R’}=\frac{\cos \theta - v/c}{1 - (v/c) \cos \theta}=\frac{c_x-v}{c-v_R}=\frac{c’_x}{c_{R’}}\)
\(\cos \theta’ =\frac{\cos \theta - v/c}{1 - (v/c) \cos \theta} <\cos \theta\)
所以\(\theta’>\theta\),即运动坐标系内发现光线向y轴聚集
\(\sin \theta’ = \frac{1}{\gamma} \frac{ \sin \theta }{ 1 - (v/c) \cos \theta }=\frac{1}{\gamma} \frac{ c \sin \theta }{ c - v \cos \theta }=\frac{1}{\gamma} \frac{ c_y }{ c - v \cos \theta }=\frac{1}{\gamma} \frac{c_y}{c_{R’}}\)
\(\sin \theta’ = \frac{\sin \theta }{\gamma(1 - (v/c) \cos \theta) }= \frac{\sin \theta R}{\gamma R’}\),即:
\(R’\sin \theta’ = \frac{R\sin \theta}{\gamma}\), 即\(y’=y/\gamma\)
\(\frac{\sin\theta}{\sin\theta’}=\frac{\gamma R’}{R}=\gamma \frac{dt}{dt’}\)
\(\frac{cdt}{cdt’}=\frac{c\sin\theta’}{\gamma c\sin\theta}=\frac{c’_y}{\gamma c_y}\)
\(\tan \theta’ = \frac{1}{\gamma} \frac{\sin \theta}{\cos \theta - v/c}=\frac{1}{\gamma} \frac{c_y}{c’_x}\)
\(y’=(x-vt)\tan \theta’=\frac{y}{\gamma}=\frac{R sin\theta}{\gamma} \)
\(\frac{x-vt}{x-vt’}=\frac{x-v(t’+R/c)}{x-vt’}=\frac{c cos\theta -v}{c cos\theta}\)
\(\frac{x-vt}{c cos\theta-v}=\frac{x-vt’}{c cos\theta}=t-t’\),即:
\(\frac{x-vt}{c’_x}=\frac{x-vt’}{c_x}=t-t’\)
可见,\(y’=y/\gamma\)的原因在于:
\(c_y’ =\frac{c_y}{\gamma}\), \(c_x’=c cos\theta-v\)
\(y’=c_y’ dt =\frac{c_y}{\gamma} dt\)
\(\sin\theta=\frac{y}{R}\)
\(\sin\theta’=\frac{y}{\gamma R’}\)
\((t-t’)\sqrt{(c-v \cos\theta)^2-(c \cos\theta-v)^2}=y/\gamma\)
在移动坐标系内向一个静止坐标系内的固定点发射一个光子,那么在静止坐标系看来,任意时刻t,相对于光源,光子的x坐标为x-vt,而y方向光的相对分量则为垂直分量的\(1/\gamma\),主要是因为y方向的分量由于x方向的运动而发生相对偏离,导致y方向的真实坐标变成了\(y/\gamma\)(这个其实仍然不确定,还没有搞清楚,仍然难以从几何上描述),而在静止坐标系内,发射光子的时间为t’, 那么光子的位置就是(x-vt’,y),这与推迟势中是一致的。
很多关系可以参考下面的图形:
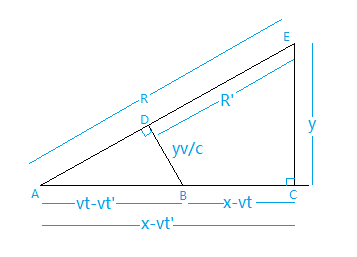
\(\overline{AE}=R\),\(\overline{DE}=R’\),\(\overline{AC}=x-vt’\),\(\overline{BC}=x-vt\),
\(\overline{BD}\)是从光源在时刻t的位置,做R的垂线,\(\overline{AB}=v(t-t’)\)
所以\(\frac{\overline{BD}}{\overline{EC}}= \frac{\overline{AE}}{\overline{AB}}\),
得:\(\overline{BD}=y \frac{v(t-t’)}{R}=y\frac{v}{c}\)
有四边形BDEC可以得出:
\(R’^2=BC^2+EC^2-BD^2=(x-vt)^2+y^2-(yv/c)^2=(x-vt)^2+(y/\gamma)^2\)
或使用三角形ABD,有:
\(\overline{AD}=(R-R’)^2=(v(t-t’))^2-(yv/c)^2\)
\(R’=R-\sqrt{((v(t-t’))^2-(yv/c)^2)}=R-\frac{v}{c}(x-vt’)\)
但仍然无法直接体现\(y/\gamma\)与\(y\)的直角关系
我们可以这样看:
三角形\(ACE\)整体减少了\((t-t’)\vec{v} \cdot \vec{p}=(t-t’)vcos\phi\),\(\phi\)是与v方向的夹角,即速度v在方向p上的点积/投影。对应减去了三角形\(ABD\),
\(R\)减少了\((t-t’) v cos(\theta)=(x-vt’) \frac{v}{c}\),即v在R上的投影,R变成了\(R’=R(1-\frac{v}{c}cos(\theta))\)
\(y\)减少了\((t-t’) v sin(\theta’’)=y\frac{v}{c}\),即由于产生了x方向的分量导致y变倾斜角度和y轴成\(sin(\theta’’)=v/c\),y变成了\(y’=\sqrt{y^2-(y\frac{v}{c})^2}=\frac{y}{\gamma}\)
\(x-vt’\)减少了\((t-t’) v cos(0)=v(t-t’)=R\frac{v}{c}\),即v在x上的投影是自身v, x变成了\(x’=x-vt’-v(t-t’)=x-vt\)
于是我们最终得到了一个由\(R’,x-vt,\frac{y}{\gamma}\)拼凑起来的三角形。上面的三条是最根本的三条,前面的所有推论皆源于此,这也是推迟势和洛伦兹变换的最直观的几何解释。
=======
我们可以这么理解:
使用任意一个光源,不属于移动坐标系,在和移动坐标系原点重合时时间为t’,发射两束光,水平方向在时刻t,与移动坐标系的原点距离为:
\(x’=x-vt=x-vt_1-v(t_2-t_1)=c(t_2-t_1)-v(t_2-t_1)=(c-v)(t_2-t_1)\),
而y方向,则需要斜着射出光线,光走的距离为c(t_2-t_1),y方向坐标:
\(y’=c(t_2-t_1)/\gamma\)
所以,实际上在静止坐标系中观察移动坐标系,y方向的光速变成了:
\(c’_y=c/\gamma=\sqrt{c^2-v^2}\),
在静止坐标系内观察,要想让y方向到达某个y’,必须使用更多的时间\(\gamma (t_2-t_1)\),位置变成了y, 但x方向距离就变成了\(\gamma(x-vt)\),时间也是\(\gamma(t_2-t_1)\),光速仍然为c,
也就是坐标由\((x-vt, y/\gamma)\),相对光速由\((c-v, c/\gamma)\),
移动坐标系内自己测的时间,以接收时间差为准,则x方向为:
x方向我们有 \(\frac{dt}{dt’}=\frac{c-v}{c}\)
\(\Delta t_x=\frac{dt}{dt’}(t_2-t_1)=(t_2-t_1)\frac{c-v}{c}\)
光的速度为\(((x-vt)/\Delta t_x=(c-v)(t_2-t_1)/\Delta t_x=c\)
y方向\(cos(\theta)=\frac{v}{c}\):
\(\frac{dt}{dt’}=1-\frac{v}{c} cos(\theta)=1/\gamma^2\)
接收到的时间为:
\(\Delta t_y=\frac{t_2-t_1}{\gamma^2}\)
测到的光速为:
\(\frac{c(t_2-t_1)/\gamma}{(t_2-t_1)/\gamma^2}=c/\gamma\),竟然不是c?
也许正确的表述应该是,移动坐标系里y轴上的测量者,测得光在自己的y轴上走了\Delta t/\gamma^2秒,同时它也知道光实际走的距离为c\Delta t, 是斜线,所以它就认为光在y轴上只走了c\Delta t/ \gamma^2=c\Delta t/\gamma /\gamma=y/\gamma,,,仍然有拼凑的嫌疑,还是没有彻底解决
那么迈克尔逊莫雷实验:有来自宇宙的两束垂直的光进入水平和垂直通道,水平通道时间为c/(c-v) L/c+c/(c+v) * L/c=2\gamma^2 L/c, 垂直通道的来回时间为2\gamma^2 L/c,这里我们采用了水平方向dt/dt’=1-v/c和1+v/c, 垂直方向dt/dt’=1/\gamma^2, 而dt为L/c,则水平方向我们计算的是dt’
从关系式:
\(c [ \gamma (t - v x / c^2) - t’ / \gamma ] = \sqrt{ \gamma^2 (x - v t)^2 + y^2 }=\gamma R’\)
是否就是洛伦兹变换
=======
在静止坐标系内观察移动坐标系:
\(\Delta t=\frac{x-vt}{c-v}\)
即:\(t_r-t_e=\frac{x-vt_r}{c-v}\)
\(t_e =t_r-\frac{x-vt_r}{c-v}\)
\(=\frac{ct_r-x}{c-v}\)
\(=(ct_r-x)\frac{c+v}{c^2}\frac{c^2}{c^2-v^2}\)
\(=\gamma^2 \frac{ct_r-x)(c+v)}{c^2}\)
\(=\gamma^2(t_r-\frac{vx}{c^2}-\frac{x-vt_r}{c})\)
\(=\gamma(\gamma(t_r-\frac{vx}{c^2})-\frac{\gamma(x-vt_r)}{c})\)
\(=\gamma(t’_r-\frac{x’}{c})\)
\(=\gamma t’_e\)
表示在发射点x’_e为0的时候,\(t_e=\gamma(t’_e+\frac{x’_e v}{c^2})=\gamma t’_e\)
所以上面我们使用到了:
\(t’_r=\gamma(t_r-\frac{xv}{c^2})\)
\(t_e=\gamma(t’_e+\frac{x’_e v}{c^2})\), 光源位置\(x’_e=0\)
\(x’=\gamma(x-vt)\)
=======
在移动坐标系内,
\(x’_r-x’_e=c(t’_r-c’_e)\),
光线接收时间\(t’_r\),发射时间\(c’_e\),接收位置\(x’_r\),发射位置\(x’_e\)
有:
\((x’_r - x’_e) (1 - \frac{v}{c}) = (t’_r - t’_e) (c - v)\),
\((x’_r - x’_e)+v(t’_r - t’_e)=c(t’_r - t’_e)+(x’_r - x’_e)\frac{v}{c}\),
\((x’_r + vt’_r)-(x’_e + vt’_e)=c(t’_r + \frac{v x’_r}{c^2})-c(t’_e + \frac{v x’_e}{c^2})\),
\(\gamma(x’_r + vt’_r)-\gamma(x’_e + vt’_e)=c(\gamma(t’_r + \frac{v x’_r}{c^2}))-c(\gamma(t’_e + \frac{v x’_e}{c^2}))\),
即:
\(x_r-x_e=c(t_r-t_e)\)
在洛伦兹变换下,推迟势中,R’中的接收时间\gamma(t-xv/c^2)对应R的t,发射时间t’/\gamma对应R的t’
=====
在静止坐标系内观察移动坐标系:
\(\Delta t=\frac{x-vt}{c-v}\)
即:\(t_r-t_e=\frac{x-vt_r}{c-v}\)
\(t_e =t_r-\frac{x-vt_r}{c-v}\)
\(=\frac{ct_r-x}{c-v}\)
\(=(ct_r-x)\frac{c+v}{c^2}\frac{c^2}{c^2-v^2}\)
\(=\gamma^2 \frac{ct_r-x)(c+v)}{c^2}\)
\(=\gamma^2(t_r-\frac{vx}{c^2}-\frac{x-vt_r}{c})\)
\(=\gamma(\gamma(t_r-\frac{vx}{c^2})-\frac{\gamma(x-vt_r)}{c})\)
\(=\gamma(t’_r-\frac{x’}{c})\)
\(=\gamma t’_e\)
表示在发射点x’_e为0的时候,\(t_e=\gamma(t’_e+\frac{x’_e v}{c^2})=\gamma t’_e\)
所以上面我们使用到了:
\(t’_r=\gamma(t_r-\frac{xv}{c^2})\)
\(t_e=\gamma(t’_e+\frac{x’_e v}{c^2})\), 光源位置\(x’_e=0\)
\(x’=\gamma(x-vt)\)
这些公式和前面的\(\gamma R’\)相同。这些公式说明了什么?
这个推导过程至少说明了,我们应该使用相同类型的时间来对比,
\(t_e\)对比\(t’_e\), \(t_r\)对比\(t’_r\),
如果我们使用了\(t_e\)对比\(t_r\)或\(t’_r\),那么可能就会丢失\(\gamma\),
使得多普勒变换的频率丢失了\(\gamma\),只是\(dt/dt’\)而不是\(\gamma dt_r/dt_e\)
=======
在移动坐标系内,
\(x’_r-x’_e=c(t’_r-c’_e)\),
光线接收时间\(t’_r\),发射时间\(c’_e\),接收位置\(x’_r\),发射位置\(x’_e\)
有:
\((x’_r - x’_e) (1 - \frac{v}{c}) = (t’_r - t’_e) (c - v)\),
\((x’_r - x’_e)+v(t’_r - t’_e)=c(t’_r - t’_e)+(x’_r - x’_e)\frac{v}{c}\),
\((x’_r + vt’_r)-(x’_e + vt’_e)=c(t’_r + \frac{v x’_r}{c^2})-c(t’_e + \frac{v x’_e}{c^2})\),
\(\gamma(x’_r + vt’_r)-\gamma(x’_e + vt’_e)=c(\gamma(t’_r + \frac{v x’_r}{c^2}))-c(\gamma(t’_e + \frac{v x’_e}{c^2}))\),
即:
\(x_r-x_e=c(t_r-t_e)\)
这个变换说明了世界线的不变量\(c\Delta t-\Delta x=0\)。这个变换的推导又说明了什么?
====
还有一个等式:
\( c^2(t-\frac{vx}{c^2})^2-(x-vt)^2=\frac{(ct)^2-x^2}{\gamma^2}=\frac{y^2}{\gamma^2}\)
也就是从等心圆\(x’^2+y’^2=(ct’)^2\)到等心圆\(x^2+y^2=(ct)^2\)
这个推导的意义,是说明\(t’=t-xv/c^2\)与\(y’=y/\gamma\)是等价的,t的缩减是由于y的缩减造成的,或者t缩减则y缩减了,这个也与光速变成了c/\gamma等价
=====
就是如果令x’=x-vt,那么这个x’并非发射位置,而是瞬时位置,也就是观察点接收到信号后的光源位置, 而我们使用的静止坐标系的x-vt’却是发射位置。这也是长度收缩的原因,在O’系看来,x-vt和x这两个点是发射位置和接收位置,是不同时的,但在O系看来,这两个位置是同时的,x-vt不是发射位置
当然,最重要的一点,是保持了观察点位置的固定,也就是y方向固定,这个是条件
那么怎么根据这句话,推导出在O’坐标系,瞬时位置为x-vt时的发射位置为\gamma(x-vt),不考虑y值相同的情况
======
我们使用\(c(t’_r-t’_e)=x-v t_r\),假设推迟距离为x-v t_r,
如果再假设不同坐标系的接收时间同步,也就是t’_r=t_r,那么有:
\(c(t_r-t’_e)=x-v t_r\),
有:\(t’_e =t_r-(x-v t_r)/c\), (1)
由于 \(c(t_r-t_e)=x-v t_e\), 有:
\(t_r=t_e + (x-v t_e)/c\), 代入(1), 有:
\(t’_e =t_e+\frac{x-v t_e}{c}-(x-v \frac{t_e+(x-v t_e)}{c})/c \)
有:
\(t’_e =t_e + \frac{v(x-v t_e)}{c^2} =\frac{t_e}{\gamma^2}+\frac{vx}{c^2}\)
\(x’=x-v t’_e=\frac{x-v t_e}{\gamma^2}=\frac{c}{c-v}(x-v t_r) \frac{c^2-v^2}{c^2}=\frac{c+v}{c}(x-v t_r)\)
如果\(x=v t_e\), 此时光线始终垂直于静止坐标系的x轴,
\(t’_e =t_e\)
如果 \(x=vt\), 此时光线始终垂直于移动坐标系的x轴,
\(t’_e =t’_r =t_r\),
\(t_r-t_e =\frac{x-v t_e}{c}=\frac{v}{c}(t_r-t_e\)
有:\(t_r=t_e\)(垂直发射), 或\(v=c\)(光子)
由于始终有 c(t’_r-t’_e)-(x-v t_r)=c(t_r-t_e)-(x-v t_e) =0,
所以一维情况下,是无法得到\(\gamma\)的,也就是在无源的波动方程里,没有y方向的波动方程里,是不能得到\(\gamma\)放大参数的,O’坐标系的\(t’_r t’_e\)可以无限制放大,只有引入y做限制,才有\gamma的出现。除非我们追求变换的统一性,在t’到t的变换和t到t’的变换里,参数是一样的,都是\gamma,就可以找到这个共同的放大参数。
=== 我们找到统一使用接收时间的变换
\(c(t’_r-t’_e)=x-v t_r\),
假设发射时间相同,\(t’_e =t_e\), 则有:
\( t’_r=t_r-\frac{v(x-v t_e)}{c^2}\)
\(x’=x-v t_r=x-v t_e-v(t_r-t_e)\),
\(x-v t_e\)作为\(x\),\(t_r-t_e\)作为\(t\),
\(x-v t_r\)作为\(x’\),\(t’_r-t_e\)作为\(t’\),
有:
\( t’_r-t_e=t_r-t_e-\frac{vx}{c^2}\), 即:
\( t’=t-\frac{v x}{c^2}\)
\( x’=x-vt\)
其反变换:
\( t=\gamma^2(t’+\frac{v x’}{c^2}\),
\( x=\gamma^2(x’+vt’\),
所以,我们为了让变换统一,需要将t’和x’的变换里扩大\gamma倍,此时t和x的变换就缩小了\gamma倍,两者就统一了,这是在一维变换下唯一能得到增大\(\gamma\)的方法了。
当然,如果\((ct’)^2-x’^2\)和\((ct)^2-x^2\)不为0,则可以得到:
\((ct’)^2-x’^2=\frac{(ct)^2-x^2}{\gamma^2}\), 而这在现实中,只要不是光子,就肯定两者不为0
==== 我们继续使用二维含y的方程来推导\(\gamma\):
\(c(t_r-t_e)=R=\sqrt{(x-v t_e)^2+y^2}\)
\(c(t’_r-t’_e)=R=\sqrt{(x-v t_r)^2+y’^2}\)
我们假设两个坐标系使用同一个发射时间,\(t_e=t’_e\)求出 \(t’_r\)于\(t_r\)的关系式:
\( t’_r=t_r-\frac{v(x-v t_e)}{c^2}\), 和一维的完全一样
但此时有y,我们有:
\((c(t’_r-t_e)^2-(x-v t_r)^2 =\frac{(c(t’_r-t_e)^2-(x-v t_r)^2}{\gamma^2}=(y/\gamma)^2\)
可见,为了让y相同,在二维情况下,我们需要将整个移动坐标系下的\(t’_r\), \(t’_e\), \(x’\)都扩大\(\gamma\)倍:
\(\gamma t’_r=\gamma(t_r-\frac{v(x-v t_e)}{c^2})\)
\(\gamma t’_e =\gamma t_e \)
\(\gamma x’ =\gamma(x-v t_r)\)
即:
\(\gamma c(t’_r-t_e)=\gamma R=\gamma \sqrt{(x-v t_r)^2+y’^2}=\sqrt{(\gamma(x-v t_r))^2+y^2}\)
更多内容参见:狭义相对论的几个问题
在移动坐标系内测量远处静止坐标系内光源发来的光,参考:推迟势逆变换