在\(t’=0\)时，有：
\( x=\gamma x’ \)
\( (ct)^2 =x^2 -x’^2 =x^2-(\frac{x}{\gamma})^2 \)
\( x^2 =(ct)^2 +x’^2 =(ct)^2+(\frac{x}{\gamma})^2 \)
\( t=\gamma \frac{vx’}{c^2} = \frac{vx}{c^2} \)
\( ct =\frac{v}{c} x \)
解释：
此时，\(x\)和\(x’\)都在光行走的这条线上投影，\(x\)的投影正好是\(ct\), \(x’\)与光的方向垂直，投影为0，即\(ct’=0\)，如下图：
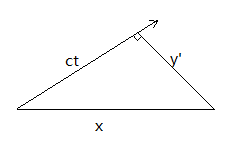
相当于把\(x\)轴和光线轴两个互换，这种情况类似快子，满足\(x=\frac{c^2}{v}t\)，在光轴上的投影为\(x_c=ct\)
在\(t=0\)时，有：
\( x’=\gamma x \)
\( (ct’)^2 =x’^2 -x^2 =x’^2-(\frac{x’}{\gamma})^2 \)
\( x’^2 =(ct’)^2 +x^2 =(ct’)^2+(\frac{x’}{\gamma})^2 \)
\( t’=-\gamma \frac{vx}{c^2} = -\frac{vx’}{c^2} \)
\( ct’ =-\frac{v}{c}x’ \)
我们假设快子的振动形成了电磁波，那么快子的波动方程是什么，怎么用来描述量子纠缠？