推迟势中:
\(\phi = \frac{q}{4\pi\varepsilon_0} \cdot \frac{1}{R \left(1 - \dfrac{v(x - v t’)}{c R} \right)}\)
\(\phi(\vec{r}, t) = \frac{1}{4\pi\varepsilon_0} \cdot \frac{q}{\sqrt{ (x - v t)^2 + (y^2 + z^2)/\gamma^2 }}=\frac{1}{4\pi\varepsilon_0} \cdot \frac{q}{R’}\)
R’是一个竖着的鸭蛋形状,y方向比x方向大,看上去是光线都朝y方向聚集
\(c(t - t’) = R = \sqrt{(x - v t’)^2 + y^2 + z^2}\)
\(R=\sqrt{(x-vt’)^2 +y^2 +z^2}\)
\(R’=\sqrt{(x-vt)^2 +(y^2 +z^2)/\gamma^2}\)
\(t = t’+ R/c\)
\(t’ = \frac{c^2 t - x v - c \sqrt{(x - v t)^2 + (1 - v^2/c^2)(y^2 + z^2)}}{c^2 - v^2}=\gamma^2 (t - \frac{x v}{c^2} - \frac{1}{c} R’)\)
\(t’ = t - \frac{\sqrt{(x - v t’)^2 + y^2 + z^2}}{c}=t-\frac{R}{c}\)
\(t - t’ = \frac{v (x - v t) + c R’}{c^2 - v^2}= \gamma^2 (\frac{v (x - v t)}{c^2} + \frac{R’}{c})\)
\(R = \frac{ \beta (x - vt) + \sqrt{ \beta^2 (x - vt)^2 + (1 - \beta^2) \rho^2 } }{1 - \beta^2} = \gamma^2 \left[ \beta (x - vt) + \sqrt{ \beta^2 (x - vt)^2 + (1 - \beta^2) \rho^2 } \right]\)
\(R = \gamma^2 (\frac{v (x - v t)}{c} + R’)=\gamma (\frac{\gamma (x - v t)v}{c} + \gamma R’)\)
\(R’=R-\frac{(x-vt’)v}{c}=\sqrt{(x-vt)^2+(y^2+z^2)/\gamma^2}\)
\(c [ \gamma (t - v x / c^2) - t’ / \gamma ] = \sqrt{ \gamma^2 (x - v t)^2 + y^2 }=\gamma R’\)
\(\frac{dt}{dt’}=\frac{R’}{R} =1-\frac{v}{c}\frac{x-vt’}{R}\)
\(\frac{dt’}{dt}=\gamma^2(1+\frac{v}{c}\frac{x-vt}{R’})\)
\((1-\frac{v}{c}\frac{x-vt’}{R})(1+\frac{v}{c}\frac{x-vt}{R’})=\frac{1}{\gamma^2}\)
\(x - v t’ = \frac{ (x - v t) + \frac{v}{c} \sqrt{(x - v t)^2 + (1 - v^2/c^2)(y^2 + z^2)} }{1 - v^2/c^2}\)
\(=\gamma^2 (x - v t + \frac{vR’}{c})\)
\((x-vt’)\frac{dt}{dt’}=R’cos(\theta)=R’\frac{x-vt’}{R}\)
\(y\frac{dt}{dt’}=R’sin(\theta)\)
\(y^2 + z^2 = c^2 (t - t’)^2 - (x - v t’)^2\)
\(\frac{dR}{dt’} = -\frac{v(x - v t’)}{R}=-vcos(\theta) \)
\(\frac{dR}{dt} = c\left(1 - \gamma^2 \left(1 + \frac{v}{c} \cdot \frac{x - v t}{R’} \right)\right) \)
\(\frac{dR’}{dt} = -\frac{v(x - v t)}{R’}=-vcos(\theta’) \)
\(\frac{dR’}{dt’} = \frac{v^2}{c} - \frac{v(x - v t’)}{R}\)
如果\(c(t-t’’)=R’\),则:
\(t’’=t’+\frac{v(x-vt’)}{c^2}\)
\(\frac{dt’’}{dt}=1+\frac{v(x-vt)}{cR’}=\frac{1}{\gamma^2}\frac{dt’}{dt}\)
\(\frac{dt’’}{dt’}=\frac{1}{\gamma^2}\)
=============================
假设光源沿着x轴以速度v匀速运动,
先考虑x轴方向:
光源离原点走一段t’时间后,发射一个光子,在时间t时观察点收到光子,观察点离原点距离x,则:
\(c(t-t’)=x-vt’\)
即:
\(t=t’+\frac{x-vt’}{c}\)
求微分:
\(\frac{dt}{dt’}=1-\frac{v}{c}=\frac{c-v}{c}\)
表明光源在\(t_1\)时发射一个光子,然后再在\(t_2\)时发射另一个光子,如果光源不运动,那么在远处观察点收到两个光子的时间间隔应该是\(t_2-t_1\),但如果光源以速度v运动,那么观察点收到的光子的时间差变成了\( \frac{c-v}{c}(t_2-t_1)\)。如果光源以光速运动,那么显然观察点收到的两个光子的时间差为0。在观察点处,光子密度变成了原来的\(\frac{c}{c-v}\)。
再考虑垂直方向:
光子沿着y轴发射,发射间隔和观察点收到的时间间隔是相同的。
考虑任意方向:
由 \(c(t-t’)=R=\vec{r}-\vec{v}t’\), \(R=\sqrt{(x-vt’)^2+y^2+z^2}\)
得:
\( \frac{dt}{dt’}=1-\frac{\mathbf{v}\cdot \mathbf{n}}{c}=1-\frac{v}{c}\frac{x-vt’}{R}\)
由\(c(t-t’)=R\)求得t’:
\(t’ = \frac{c^2 t - x v - c\sqrt{(x - v t)^2 + (1 - v^2/c^2)(y^2 + z^2)}}{c^2 - v^2}\)
代入上式,则得:
\( \frac{dt}{dt’} =\frac{R’}{R} \)
\( R’=\sqrt{(x-vt)^2 + (y^2 + z^2)/\gamma^2 } \)
\( R=\sqrt{(x-vt’)^2 + y^2 + z^2} \)
\( =\gamma^2 (\frac{v}{c}( x - v t ) + \sqrt{(x - v t)^2 + (y^2 + z^2)/\gamma^2})\)
即:\(R’=R\frac{dt}{dt’}=R(1-\frac{\vec{n} \cdot \vec{v}}{c}) \)
则:
\(\frac{dt’}{dt}=\frac{R}{R’} = \gamma^2 \left( 1 + \frac{v (x - v t)}{c R’} \right)\)
同理,此时在观察点,由于接收到光子的间隔时间变化了,光子的密度变成了原来的\(\frac{dt}{dt’}\)的倒数倍
由\(R’=R(1-\frac{v(x-vt’)}{cR}\)),\(t=t’+\frac{R}{c}\)可得:
\( \gamma R’ =\frac{R}{\gamma}-\frac{v}{c}\gamma(x-vt)\)
可得:
\(y^2+z^2=(\gamma R’)^2-\gamma^2(x-vt)^2 \)
\(=R^2-(x-vt’)^2\)
\(=(c(t-t’))^2-(x-vt’)^2\)
令\(t’=0, x’=\gamma(x-vt)\),则变为:
\( (\gamma R’)^2-x’^2 =(ct)^2-x^2 \)
\(\gamma R’=\sqrt{x’^2+y^2+z^2}\)
如果令\(ct’=\gamma R’=\sqrt{x’^2+y^2+z^2}\),
可得:\((ct’)^2-x’^2=(ct)^2-x^2\)
另外还有公式:
\(\frac{dt’}{dt} = \frac{c^2(t - t’)}{c^2(t - t’) - v (x - v t’)}\)
\(\frac{dt}{dt’}=1-\frac{v(x-vt’)}{cR} = 1- \frac{v}{c} \frac{x - v t’}{c(t-t’)}\)
\(x=vt’\)时,\(\frac{dt}{dt’}=1\)
也就是垂直发射光线时,两者时间差相等(发射时间间隔和接收时间间隔)
\(\frac{dt’}{dt} = \frac{c^2 - v \frac{dx}{dt}}{c^2 - v^2} - \frac{c \left[(x - v t)(\frac{dx}{dt} - v) + (1 - v^2/c^2)\left(y \frac{dy}{dt} + z \frac{dz}{dt}\right)\right]}{(c^2 - v^2) \sqrt{(x - v t)^2 + (1 - v^2/c^2)(y^2 + z^2)}}\)
x,y,z为常数时有:
\(\frac{dt’}{dt} = \frac{c^2}{c^2 - v^2} + \frac{c v (x - v t)}{(c^2 - v^2) \sqrt{(x - v t)^2 + (1 - v^2/c^2)(y^2 + z^2)}}\)
\( = \gamma^2 \left( 1 + \frac{v (x - v t)}{c R’} \right)\)
\(y=z=0,x>vt\)时,
\(\frac{dt’}{dt}=\gamma^2\frac{c+v}{c}\)
\(y=z=0,x<vt\)时,
\(\frac{dt’}{dt}=\gamma^2\frac{c-v}{c}\)
\(x=vt\)时,\(\frac{dt’}{dt}=\gamma^2\)
\(x=vt,z=0\)时:
\(t’=t-\frac{y}{\sqrt{c^2-v^2}}\)
\(x-vt’=\frac{vy}{\sqrt{c^2-v^2}}=\gamma y \frac{v}{c}\),
可见 \(x-vt’\)与\(y\)、\(\gamma y=c(t-t’)\)呈直角三角形,说明电场分解成了x,y方向两个场。
推迟势:
\(\phi(\mathbf{r}, t) = \frac{q}{4\pi \epsilon_0} \frac{1}{\sqrt{(x - v t)^2 + (1 - \beta^2)(y^2 + z^2)}}\)
由前面的计算,可得:
\(\phi(\mathbf{r}, t) = \frac{q}{4\pi \epsilon_0} \frac{1}{R’}\)
\(=\frac{q}{4\pi \epsilon_0} \frac{\gamma}{ct’}\)
\(\mathbf{A}(\mathbf{r}, t) = \frac{\mathbf{v}}{c^2} \phi(\mathbf{r}, t)\)
\(\nabla \phi = -\frac{q \gamma}{4\pi \epsilon_0} \cdot \frac{ \left( \gamma^2 (x - v t), y, z \right) }{ \left[ \gamma^2 (x - v t)^2 + y^2 + z^2 \right]^{3/2} }\)
\(\frac{\partial \mathbf{A}}{\partial t} = \frac{q \gamma v^2}{4\pi \epsilon_0 c^2} \cdot \frac{ (\gamma^2(x - v t), 0, 0) }{ \left[ \gamma^2 (x - v t)^2 + y^2 + z^2 \right]^{3/2} }\)
\(\mathbf{E} = -\nabla \phi - \frac{\partial \mathbf{A}}{\partial t}\)
\(=\frac{q \gamma}{4\pi \epsilon_0} \cdot \frac{(x - v t, y, z)}{\left[ \gamma^2 (x - v t)^2 + y^2 + z^2 \right]^{3/2}}\)
\(\mathbf{B} = \nabla \times \mathbf{A} =\frac{q \gamma^2 v}{4\pi\epsilon_0 c^2}\frac{(0, -z, y)}{ \left[ \gamma^2 (x - vt)^2 + y^2 + z^2 \right]^{3/2}} \)
静电场: \(\mathbf{E_0} = \frac{q}{4\pi \epsilon_0} \frac{(\gamma (x - v t), y, z)}{[\gamma^2 (x - v t)^2 + y^2 + z^2]^{3/2}}\)
符合关系:
\(E^2 = (cB)^2 + E_0^2\)
\(|\mathbf{E}|^2 = E_{\parallel}^2 + \gamma^2 E_{\perp}^2 \)
\(= (E_0 \cos\theta)^2 + \gamma^2 (E_0 \sin\theta)^2 \)
\(= E_0^2 \left( \cos^2\theta + \gamma^2 \sin^2\theta \right) \)
\(= \gamma^2 |\mathbf{E}_0|^2 \cdot (1 - \beta^2 \cos^2\theta)\)
其中 \(\theta\) 是速度 \(v\) 与位矢 \(r\) 之间的夹角
附图:

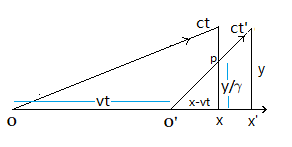
\(ct"=\gamma R’\)
======
== \(R=c(t_r-t_e)=\sqrt{(x-v t_e)^2+y^2}\):
\(\frac{dt_r}{dt_e} = 1 - \frac{v}{c} \cos\theta \), \(cos(\theta)=\frac{x-v t_e}{R}\)
\(\frac{dt_e}{dt_r} = \gamma^2 \left(1 + \frac{v}{c} \cos\theta’ \right) \), \(cos(\theta’)=\frac{x-v t_r}{R’}\), \(R’=\sqrt{(x-v t_r)^2+(y/\gamma)^2}\)
== \(R’=c(t’_r-t’_e)=\sqrt{(x-v t_r)^2+(y/\gamma)^2}\):
\(\frac{dt’_e}{dt’_r} = 1 + \frac{v}{c}\frac{x-v t_r}{R’} \),
\(\frac{dt’_r}{dt’_e} = \gamma^2 \left(1 - \frac{v}{c}\frac{x-v t_e}{R} \right)\),
\(t’_e =t_r\), \(t’_r =t_r+\frac{R’}{c}\)
\(\frac{dt_r}{dt’_e}=1\)
\(\frac{dt’_e}{dt_e}=\frac{dt_r}{dt_e}\)
\(\frac{dt’_r}{dt’_e}=\frac{dt’_r}{dt_r}=1-\frac{v}{c}cos(\theta’)\)
== \(R_g =c(t’_r-t’_e)=\sqrt{\gamma^2(x-v t_r)^2+y^2}\):
\(\frac{dt’_e}{dt’_r} = 1 + \frac{v}{c}\frac{\gamma^2 (x-v t_r)}{R_g}= 1 + \frac{\gamma v cos(\theta_g)}{c}1 + \frac{\gamma v cos(\theta’)}{c}\)
\(t’_e =(x-\gamma(x-v t_r))/v=t_r + \frac{(x - v t_r)(1 - \gamma)}{v}\),
\(t’_r = t’_e + \frac{1}{c} \sqrt{ \gamma^2 (x - v t_r)^2 + y^2 }\)
\( \frac{dt’_r}{dt_r}=\gamma(1-\frac{v \gamma (x-v t_r)}{c R_g})\)
\(\frac{dt’_e}{dt_r}=\gamma \),而R’的\(\frac{dt_e}{dt_r}=1 \)
\(\frac{dt’_e}{dt_e}=\gamma \frac{dt_r}{dt_e}=\gamma (1-\frac{vcos(\theta)}{c}) \),
\( \frac{dt’_r}{dt_e}=\gamma(1-\frac{v \gamma (x-v t_r)}{c R_g})\frac{dt_r}{dt_e}=\gamma(1-\frac{v }{c}cos(\theta’))\frac{dt_r}{dt_e}\)
\(\frac{dt’_r}{dt’_e} = 1 - \frac{v}{c} \cos\theta_g=1 - \frac{v}{c} \cos\theta’\)
\((1+\frac{v}{c} cos(\theta’)) * (1-\frac{v}{c} cos(\theta))=\frac{1}{\gamma^2}\)
\(\frac{t’_r-t’_e}{t_r-t_e}=\frac{\gamma R’}{R}=\gamma(1-\frac{v}{c}cos(\theta))\)