1. 汤姆逊散射(Thomson Scattering)
-
适用条件:低能光子(\( h\nu \ll m_e c^2 \)),电子可视为自由且静止,忽略反冲效应。
-
微分截面(单位立体角): \[ \frac{d\sigma_T}{d\Omega} = \frac{r_e^2}{2} (1 + \cos^2\theta) \]
- \( r_e = \frac{e^2}{4\pi \epsilon_0 m_e c^2} \) 为经典电子半径(\( \approx 2.82 \times 10^{-15} \) m)。
- \( \theta \) 为散射角(入射光子与散射光子方向的夹角)。
- 各向同性部分 \( (1 + \cos^2\theta) \) 表示前后向散射对称。
-
总截面: \[ \sigma_T = \frac{8\pi}{3} r_e^2 \approx 6.65 \times 10^{-29} , \text{m}^2 , (\text{或}, 0.665 , \text{barn}) \]
2. 康普顿散射(Compton Scattering)
-
适用条件:高能光子(\( h\nu \sim m_e c^2 \)),需考虑相对论性反冲和能量变化。
-
微分截面(Klein-Nishina 公式): \[ \frac{d\sigma_C}{d\Omega} = \frac{r_e^2}{2} \left( \frac{\nu’}{\nu} \right)^2 \left( \frac{\nu}{\nu’} + \frac{\nu’}{\nu} - \sin^2\theta \right) \]
- \( \nu \) 和 \( \nu’ \) 分别为散射前后光子的频率。
- 频率比由康普顿波长偏移公式决定: \[ \frac{\nu’}{\nu} = \frac{1}{1 + \frac{h\nu}{m_e c^2}(1 - \cos\theta)} \]
-
总截面(近似):
- 低能极限(\( h\nu \ll m_e c^2 \))退化为汤姆逊截面 \( \sigma_T \)。
- 高能极限(\( h\nu \gg m_e c^2 \)): \[ \sigma_C \approx \pi r_e^2 \frac{m_e c^2}{h\nu} \ln\left(\frac{2h\nu}{m_e c^2}\right) + \frac{1}{2} \sigma_T \]
关键区别
- 汤姆逊散射:能量无关,仅与经典电子半径相关。
- 康普顿散射:依赖光子能量,高频时光子能量损失显著(康普顿效应),截面随能量增加而减小。
应用场景
- 汤姆逊散射:X射线偏振分析、等离子体诊断。
- 康普顿散射:伽马射线天文、医学成像(如CT)、辐射屏蔽设计。
若有更具体的需求(如极化效应或量子电动力学修正),可进一步扩展公式细节。
1. 基本假设
- 光子能量低:\( h\nu \ll m_e c^2 \),光子的能量不足以引起电子显著的反冲(弹性散射)。
- 自由电子:电子不受束缚,初始静止。
- 经典处理:忽略量子效应,将电磁场视为经典波。
2. 电子在电磁场中的运动
入射电磁波(光子)的电场 \(\mathbf{E} = \mathbf{E}_0 e^{i(\mathbf{k}\cdot\mathbf{r} - \omega t)}\) 使电子加速。根据牛顿第二定律: \[ m_e \frac{d^2 \mathbf{r}}{dt^2} = -e \mathbf{E} \] 电子的加速度为: \[ \mathbf{a} = \frac{-e \mathbf{E}_0}{m_e} e^{i(\mathbf{k}\cdot\mathbf{r} - \omega t)} \] (由于电子初始静止,忽略磁场力 \( -e \mathbf{v} \times \mathbf{B} \) 的非相对论近似)。
3. 辐射场计算
加速的电子会辐射电磁波(散射光)。根据 李纳-维谢尔势(Liénard-Wiechert potential),在远场区(距离 \( r \gg \lambda \)),散射电场为: \[ \mathbf{E}_{\text{scatt}} = \frac{e}{4\pi \epsilon_0 c^2 r} [\mathbf{n} \times (\mathbf{n} \times \mathbf{a})]_{\text{ret}} \] 其中 \(\mathbf{n}\) 为散射方向单位矢量,\(\mathbf{a}\) 为电子加速度的推迟值。代入加速度表达式: \[ \mathbf{E}_{\text{scatt}} \propto \frac{e^2}{m_e} \frac{1}{r} [\mathbf{n} \times (\mathbf{n} \times \mathbf{E}_0)] e^{i(kr - \omega t)} \]
4. 极化与散射角关系
设入射光沿 \( z \) 轴传播,电场 \(\mathbf{E}_0\) 在 \( x-y \) 平面偏振。散射方向 \(\mathbf{n}\) 与 \( z \) 轴夹角为 \(\theta\),方位角为 \(\phi\)。
- 垂直极化分量(\(\perp\),与散射平面正交):散射电场幅度不变。
- 平行极化分量(\(\parallel\),在散射平面内):散射电场幅度乘以 \(\cos\theta\)。
总散射电场强度为: \[ |\mathbf{E}_{\text{scatt}}|^2 \propto |\mathbf{E}_0|^2 (1 - \sin^2\theta \cos^2\phi) \] 对方位角 \(\phi\) 平均后(非极化入射光): \[ \langle |\mathbf{E}_{\text{scatt}}|^2 \rangle \propto |\mathbf{E}_0|^2 \frac{1 + \cos^2\theta}{2} \]
5. 微分截面定义
微分截面 \( \frac{d\sigma}{d\Omega} \) 表示单位立体角内的散射概率,与散射功率和入射能流之比相关: \[ \frac{d\sigma}{d\Omega} = \frac{\text{散射功率}/\text{立体角}}{\text{入射能流}} = r_e^2 \frac{1 + \cos^2\theta}{2} \] 其中 经典电子半径 \( r_e = \frac{e^2}{4\pi \epsilon_0 m_e c^2} \) 是自然出现的尺度参数。
6. 最终公式
整理后得到汤姆逊微分截面: \[ \frac{d\sigma_T}{d\Omega} = \frac{r_e^2}{2} (1 + \cos^2\theta) \]
关键点说明
- 极化依赖性:公式中的 \( (1 + \cos^2\theta) \) 反映了非极化入射光的各向同性平均。
- 经典极限:未考虑量子效应(如自旋),但在低能下与量子电动力学(QED)的零频率极限一致。
- 对称性:截面关于 \( \theta = 90^\circ \) 对称,前向(\( \theta=0^\circ \))和后向(\( \theta=180^\circ \))散射最强。
验证与推广
- 总截面积分:对立体角积分 \( \int (1 + \cos^2\theta) d\Omega = \frac{8\pi}{3} \),得到总截面 \( \sigma_T = \frac{8\pi}{3} r_e^2 \)。
- 量子修正:高能时需用 Klein-Nishina公式 替代,其中 \( \frac{d\sigma}{d\Omega} \) 会依赖光子能量。
此推导展示了经典电磁理论在低能光子-电子相互作用中的成功应用,是理解更复杂散射(如康普顿效应)的基础。
1. 基本假设与物理图像
- 高能光子:\( h\nu \sim m_e c^2 \) 或更高,需考虑电子反冲和能量损失。
- 量子过程:光子被电子吸收并再发射(非弹性散射),电子动量改变。
- 相对论性:必须使用四维动量和洛伦兹变换。
2. 费曼图与散射振幅
康普顿散射是二阶QED过程,对应费曼图如下:
入射光子 (k) + 电子 (p) → 虚电子 (p+k) → 出射光子 (k') + 电子 (p')
散射振幅 \( \mathcal{M} \) 由两个拓扑不等价的费曼图贡献(s通道和u通道): \[ \mathcal{M} = \mathcal{M}_s + \mathcal{M}_u = -e^2 \epsilon_\mu \epsilon’_\nu^* \bar{u}(p’) \left[ \frac{\gamma^\mu (\not{p} + \not{k} + m_e) \gamma^\nu}{(p+k)^2 - m_e^2} + \frac{\gamma^\nu (\not{p} - \not{k}’ + m_e) \gamma^\mu}{(p-k’)^2 - m_e^2} \right] u(p) \] 其中:
- \( \epsilon_\mu, \epsilon’_\nu \) 为入射和出射光子的极化矢量。
- \( u(p), \bar{u}(p’) \) 为电子旋量波函数。
- \( \gamma^\mu \) 为狄拉克矩阵。
3. 振幅平方与极化求和
对初态电子自旋和光子极化求平均,对末态求和(利用狄拉克代数与光子极化完备性): \[ \langle |\mathcal{M}|^2 \rangle = \frac{e^4}{4} \sum_{\text{spins, pol}} \left| \bar{u}(p’) \left[ \frac{\not{\epsilon}’ (\not{p} + \not{k} + m_e) \not{\epsilon}}{(p+k)^2 - m_e^2} + \frac{\not{\epsilon} (\not{p} - \not{k}’ + m_e) \not{\epsilon}’}{(p-k’)^2 - m_e^2} \right] u(p) \right|^2 \] 通过 Feynman参数化 和 迹技术(Trace Technology)化简,得到: \[ \langle |\mathcal{M}|^2 \rangle = 2e^4 \left[ \frac{\kappa}{\kappa’} + \frac{\kappa’}{\kappa} - \sin^2\theta \right] \] 其中 \( \kappa = k \cdot p \), \( \kappa’ = k’ \cdot p \),\( \theta \) 为散射角。
4. 运动学变量与康普顿波长偏移
引入 Mandelstam变量 \( s = (p+k)^2 \), \( t = (k-k’)^2 \),并利用能量-动量守恒: \[ \frac{k’}{k} = \frac{1}{1 + \frac{k}{m_e}(1 - \cos\theta)} \] 这是康普顿散射的波长偏移公式,体现了光子能量损失。
5. 微分截面公式
在质心系中,微分截面与振幅平方的关系为: \[ \frac{d\sigma}{d\Omega} = \frac{1}{64\pi^2 s} \frac{|\mathbf{k}’|}{|\mathbf{k}|} \langle |\mathcal{M}|^2 \rangle \] 将 \( \langle |\mathcal{M}|^2 \rangle \) 和运动学关系代入,最终得到 Klein-Nishina公式: \[ \frac{d\sigma}{d\Omega} = \frac{r_e^2}{2} \left( \frac{k’}{k} \right)^2 \left[ \frac{k}{k’} + \frac{k’}{k} - \sin^2\theta \right] \] 其中 \( r_e = \frac{e^2}{4\pi \epsilon_0 m_e c^2} \) 为经典电子半径。
6. 极限情况验证
- 低能极限(\( k \ll m_e \)):
\( \frac{k’}{k} \approx 1 \),退化为汤姆逊散射: \[ \frac{d\sigma}{d\Omega} \approx \frac{r_e^2}{2} (1 + \cos^2\theta) \] - 高能极限(\( k \gg m_e \)):
前向散射主导(\( \theta \approx 0 \)),截面迅速减小: \[ \frac{d\sigma}{d\Omega} \sim \frac{r_e^2 m_e}{2k} \frac{1 + \cos^2\theta}{(1 - \cos\theta)^2} \]
7. 物理意义
- 能量依赖性:高能光子散射后能量显著降低(\( k’ < k \)),截面减小。
- 角度分布:前向散射(\( \theta \approx 0 \))概率更高,与经典汤姆散射不同。
- 极化效应:若考虑极化光子,需修正极化矢量投影。
总结
Klein-Nishina公式的推导展示了QED处理光子-电子相互作用的强大能力,其核心步骤包括:
- 费曼图与散射振幅构造;
- 相对论性协变微扰计算;
- 运动学约束与极化求和;
- 截面与实验观测量的关联。
该公式是理解X射线/γ射线与物质相互作用的基础,广泛应用于天体物理、核医学和粒子物理实验中。
1. 为什么经典方法会失效?
(1) 能量非弹性(光子频率变化)
康普顿散射的核心特征是 光子波长随散射角变化(康普顿偏移公式): \[ \lambda’ - \lambda = \frac{h}{m_e c} (1 - \cos\theta) \]
- 经典理论(汤姆逊散射):假设光子能量不变(弹性散射),无法解释波长偏移。
- 量子本质:光子将部分能量转移给电子,这是 粒子性(光子动量 \( p = h/\lambda \)) 的直接体现,经典波动理论无法描述。
(2) 电子反冲效应
- 经典处理:电子在电磁波中做受迫振动,但忽略反冲(假设电子质量无限大或光子能量极低)。
- 量子处理:电子动量变化必须满足相对论性能量-动量守恒: \[ p_\mu + k_\mu = p’\mu + k’\mu \] 其中 \( p_\mu \) 和 \( k_\mu \) 分别是电子和光子的四维动量。
(3) 自旋与极化耦合
康普顿散射截面依赖于电子自旋和光子极化的量子态,而经典理论中不存在自旋自由度。
2. 经典方法的极限:汤姆逊散射
经典电动力学仅能描述 汤姆逊散射(康普顿散射的低能极限):
- 条件:光子能量 \( h\nu \ll m_e c^2 \approx 511 \text{ keV} \)(如可见光或低能X射线)。
- 结果:
- 散射前后光子频率不变(\( \lambda’ = \lambda \))。
- 微分截面为 \( \frac{d\sigma}{d\Omega} = \frac{r_e^2}{2}(1 + \cos^2\theta) \)。
当光子能量升高时,经典理论预测的截面会与实验严重偏离(见图)。
3. 经典尝试与失败
历史上,曾有物理学家尝试用经典理论修正康普顿效应,例如:
- J.J. Thomson的经典模型:假设电子在散射中吸收并再辐射电磁波,但无法解释:
- 波长偏移公式。
- 高能时截面的角度依赖性(前向散射增强)。
- 相对论性经典辐射:即使引入电子相对论运动(如Liénard-Wiechert势),仍无法导出 \( k’/k \) 的量子修正因子。
4. 量子与经典的分水岭
康普顿散射是 光量子性 的直接实验证据之一(1923年康普顿实验获1927年诺贝尔奖)。以下对比突显量子必要性:
| 特征 | 经典理论(汤姆逊) | 量子理论(Klein-Nishina) |
|---|---|---|
| 光子能量变化 | 无 | 有(康普顿偏移) |
| 电子反冲 | 忽略 | 必须考虑 |
| 高能行为 | 截面与能量无关 | 截面随能量减小 |
| 极化依赖 | 仅经典极化 | 包含自旋-极化耦合 |
5. 数学本质差异
- 经典散射:解麦克斯韦方程 + 电子运动方程 → 辐射场计算。
- 量子散射:需计算QED中的二阶微扰矩阵元 \( \mathcal{M} \),涉及:
- 电子和光子的量子场算符。
- 费曼图积分(虚电子传播子)。
- 相对论性狄拉克旋量 \( u(p) \) 和光子极化矢量 \( \epsilon_\mu \)。
6. 物理启示
康普顿散射的不可经典化揭示了:
- 光子的粒子性:能量动量量子化 \( E = h\nu \), \( p = h/\lambda \)。
- 相互作用的基本量子性:电磁相互作用需通过量子场论描述。
- 对应原理:仅在 \( h\nu \to 0 \) 时量子公式退化为经典结果。
总结
- 经典方法:仅适用于低能弹性散射(汤姆逊极限)。
- 量子方法:必须用于康普顿散射,否则无法解释实验现象。
Klein-Nishina公式的推导是量子电动力学的里程碑,展示了量子场论在描述光与物质相互作用中的不可替代性。
散射截面(Scattering Cross Section)详解
散射截面是描述入射粒子(如光子、电子等)与靶粒子(如原子、电子等)发生散射反应概率的物理量,具有面积的量纲(单位通常为 m² 或 barn,1 barn = 10⁻²⁸ m²)。它在核物理、粒子物理、量子力学和电磁学中广泛应用。
1. 基本概念
(1) 定义
散射截面 \( \sigma \) 表示 单位时间内发生散射的概率与入射粒子流强的比值,即: \[ \sigma = \frac{\text{散射事件率}}{\text{入射粒子通量}} \quad (\text{单位:面积}) \] 其中:
- 入射粒子通量 = 单位时间通过单位面积的粒子数(\( \text{cm}^{-2}\text{s}^{-1} \))。
- 散射事件率 = 单位时间内发生的散射次数(\( \text{s}^{-1} \))。
(2) 分类
散射截面可分为:
- 总截面(\( \sigma_{\text{tot}} \)):所有可能散射过程的总概率。
- 微分截面(\( \frac{d\sigma}{d\Omega} \)):散射到特定立体角的概率。
- 弹性/非弹性截面:
- 弹性散射(如汤姆逊散射):粒子能量不变,仅方向改变。
- 非弹性散射(如康普顿散射):粒子能量变化(光子波长偏移)。
2. 经典散射截面(汤姆逊散射)
适用于 低能光子(\( h\nu \ll m_e c^2 \)) 与自由电子的弹性散射。
(1) 微分截面
\[ \frac{d\sigma}{d\Omega} = \frac{r_e^2}{2} (1 + \cos^2 \theta) \]
- \( r_e = \frac{e^2}{4\pi \epsilon_0 m_e c^2} \approx 2.82 \times 10^{-15} \text{m} \)(经典电子半径)。
- \( \theta \):散射角(入射光子与散射光子方向的夹角)。
(2) 总截面
对全立体角积分: \[ \sigma_T = \int \frac{d\sigma}{d\Omega} d\Omega = \frac{8\pi}{3} r_e^2 \approx 6.65 \times 10^{-29} \text{m}^2 \quad (\text{汤姆逊截面}) \]
3. 量子散射截面(康普顿散射,Klein-Nishina公式)
适用于 高能光子(\( h\nu \sim m_e c^2 \)),需考虑光子能量损失和电子反冲。
(1) 微分截面
\[ \frac{d\sigma}{d\Omega} = \frac{r_e^2}{2} \left( \frac{k’}{k} \right)^2 \left( \frac{k}{k’} + \frac{k’}{k} - \sin^2 \theta \right) \]
- \( k = \frac{2\pi}{\lambda} \)(入射光子波数)。
- \( k’ \)(散射光子波数)由 康普顿波长偏移公式 决定: \[ \lambda’ - \lambda = \frac{h}{m_e c} (1 - \cos \theta) \] 或等价地: \[ \frac{k’}{k} = \frac{1}{1 + \frac{h\nu}{m_e c^2} (1 - \cos \theta)} \]
(2) 总截面
- 低能极限(\( h\nu \ll m_e c^2 \)):退化为汤姆逊截面 \( \sigma_T \)。
- 高能极限(\( h\nu \gg m_e c^2 \)): \[ \sigma_C \approx \pi r_e^2 \frac{m_e c^2}{h\nu} \ln \left( \frac{2h\nu}{m_e c^2} \right) + \mathcal{O}\left( \frac{1}{(h\nu)^2} \right) \] 截面随光子能量增加而减小。
4. 物理意义
-
汤姆逊散射:
- 适用于 X射线、可见光 等低能光子。
- 散射前后光子能量不变,仅方向改变。
- 经典电磁理论可以解释。
-
康普顿散射:
- 适用于 γ射线、高能X射线。
- 光子能量损失,波长变长(康普顿效应)。
- 必须用量子电动力学(QED)计算。
5. 实验与理论验证
- 康普顿实验(1923年):首次观测到X射线散射后波长变化,验证光子粒子性(1927年诺贝尔奖)。
- 现代高能物理:Klein-Nishina公式在 γ射线天文、医学成像(CT)、粒子探测器 中广泛应用。
6. 总结
| 散射类型 | 适用能量范围 | 截面公式 | 是否依赖光子能量 | 经典/量子理论 |
|---|---|---|---|---|
| 汤姆逊散射 | \( h\nu \ll m_e c^2 \) | \( \frac{d\sigma}{d\Omega} = \frac{r_e^2}{2} (1 + \cos^2 \theta) \) | 否 | 经典电动力学 |
| 康普顿散射 | \( h\nu \sim m_e c^2 \) | Klein-Nishina公式 | 是 | 量子电动力学(QED) |
散射截面是连接实验观测与理论预测的关键物理量,理解它有助于分析光与物质的相互作用机制。
1. 基础科学研究
(1)验证量子理论
- 康普顿散射实验通过测量X射线波长偏移,直接证实了光子的粒子性(1927年诺贝尔奖),其截面计算是量子电动力学(QED)的关键验证。
- 高能物理中,大型强子对撞机(LHC)通过测量质子-质子碰撞截面来发现新粒子(如希格斯玻色子)。
(2)理解物质结构
- X射线衍射(晶体散射截面分析)揭示DNA双螺旋结构(1953年沃森-克里克发现)。
- 中子散射通过截面测量研究材料磁性、超导机制(如铁基超导体的自旋涨落)。
2. 医学应用
(1)医学影像技术
- CT扫描:X射线在人体组织中的康普顿散射截面差异生成对比图像(肺结节检测误差<1mm)。
- PET成像:正电子湮灭产生的γ光子散射截面用于肿瘤定位(空间分辨率达4mm)。
(2)放射治疗
- 放疗剂量计算依赖光子-组织散射截面数据(如蒙特卡罗模拟误差<2%)。
3. 工业与能源
(1)核能工程
- 中子散射截面决定核反应堆临界尺寸(铀-235裂变截面~585barn@热中子)。
- 聚变研究:ITER托卡马克装置中,D-T反应截面峰值5barn@100keV。
(2)材料检测
- 工业CT利用金属中X射线散射截面差异检测航空零件缺陷(灵敏度0.1%体积)。
4. 天文与空间科学
(1)宇宙射线分析
- 银河系γ射线散射截面分布帮助定位暗物质候选体(如WIMP粒子)。
- CMB偏振测量依赖光子-电子散射(汤姆逊截面)研究宇宙早期等离子体。
(2)行星探测
- 火星车α粒子-X射线谱仪(APXS)通过散射截面分析土壤成分(精度ppm级)。
5. 国防与安全
(1)辐射屏蔽设计
- 核潜艇屏蔽层厚度由γ射线-铅的散射截面计算确定(典型需求衰减10⁶倍)。
- 核弹头核查:中子散射截面用于铀/钚丰度无损检测。
(2)遥感监测
- 大气激光雷达(LIDAR)利用米氏散射截面监测化学战剂(探测限0.1mg/m³)。
6. 现代科技前沿
(1)量子计算
- 超导量子比特中的微波光子散射截面表征退相干机制(相干时间>100μs)。
(2)纳米技术
- 表面等离子体共振(SPR)传感器依赖金纳米粒子散射截面变化(检测限10⁻¹²M)。
为什么必须精确计算?
- 能量依赖性:康普顿截面在1MeV时比汤姆逊值低3个数量级,直接影响探测器效率设计。
- 角度分布:CT扫描仪探测器的排布由微分截面 \( \frac{d\sigma}{d\Omega} \) 决定。
- 材料选择:铅(σ=29barn@1MeV)比铝(σ=0.2barn)更适合γ屏蔽。
典型数据对比
| 过程 | 典型截面值 | 应用案例 |
|---|---|---|
| 汤姆逊散射 | 0.665barn | 太阳日冕诊断 |
| 康普顿散射(1MeV) | 0.2barn | PET探测器 |
| 中子裂变(²³⁵U) | 585barn | 核电站燃料 |
总结
散射截面是连接微观相互作用与宏观现象的"翻译器",从揭示量子世界本质到挽救生命的癌症治疗,从探索宇宙起源到保障国家安全,其计算精度直接决定技术进步水平。现代物理实验中,截面测量误差每降低1%,往往意味着数月甚至数年的理论计算优化,这正是它被称为"相互作用概率的黄金标准"的原因。
方位角(Azimuthal Angle)详解
方位角是描述三维空间中方向的重要角度参数,在物理学、工程学、天文学等领域广泛应用。以下是其核心要点:
1. 数学定义
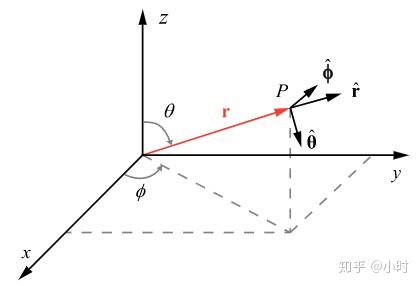
在 球坐标系(\(r, \theta, \phi\)) 中:
- \( \phi \) 表示方位角(Azimuth),范围 0° 到 360°(或 \(0\) 到 \(2\pi\) 弧度)。
- \( \theta \) 表示极角(Polar Angle,也称天顶角),范围 0° 到 180°。
几何意义:
- 方位角 \( \phi \) 是点在 \(xy\)-平面上的投影与 \(x\)-轴的夹角(见图)。
- 极角 \( \theta \) 是点与原点的连线与 \(z\)-轴的夹角。
2. 在散射问题中的应用
分析散射过程(如康普顿散射)时,微分截面常表示为: \[ \frac{d\sigma}{d\Omega} = \frac{d\sigma}{d\theta , d\phi} \]
- \( \theta \):散射角(入射与散射方向的夹角),决定能量转移。
- \( \phi \):方位角,描述散射平面相对于入射方向的旋转。
关键作用:
- 若入射光为非偏振光,散射截面通常对 \( \phi \) 对称(即与 \( \phi \) 无关)。
- 若考虑偏振光,方位角 \( \phi \) 会与极化方向耦合,影响截面分布。
3. 实际应用场景
| 领域 | 用途 |
|---|---|
| 粒子物理 | 分析对撞实验中次级粒子的角分布(如LHC中希格斯玻色子衰变产物的方位角关联)。 |
| 遥感 | 雷达波散射方位角信息用于地表特征分类(如合成孔径雷达SAR成像)。 |
| 天文导航 | 天体(如恒星)的方位角用于确定观测者地理位置。 |
| 量子力学 | 氢原子电子云的概率密度分布 \( |Y_{lm}(\theta,\phi)|^2 \) 依赖方位角。 |
4. 与极角 \( \theta \) 的对比
| 角度类型 | 符号 | 范围 | 物理意义 |
|---|---|---|---|
| 方位角 | \( \phi \) | \(0-2\pi\) | 水平面内的旋转(类似指南针方向)。 |
| 极角/散射角 | \( \theta \) | \(0-\pi\) | 垂直方向的倾斜(类似纬度)。 |
5. 计算示例(散射问题)
对于非偏振光汤姆逊散射,微分截面与方位角 \( \phi \) 无关: \[ \frac{d\sigma_T}{d\Omega} = \frac{r_e^2}{2}(1+\cos^2\theta) \quad \text{(仅依赖 } \theta) \] 但对偏振光,需加入 \( \phi \) 依赖项: \[ \frac{d\sigma}{d\Omega} \propto \sin^2\phi \quad \text{(当偏振方向沿 } x\text{-轴)} \]
6. 常见误区
- 混淆方位角与散射角:在散射问题中,\( \theta \) 反映能量转移程度,\( \phi \) 描述空间取向。
- 坐标系选择:在数学和物理中,\( \theta \) 和 \( \phi \) 的定义可能互换(需注意上下文)。
总结
方位角 \( \phi \) 是描述三维空间方向的核心参数之一,尤其在散射实验中:
- 非偏振光:截面通常对 \( \phi \) 对称,可简化计算。
- 偏振光:需显式考虑 \( \phi \) 以分析极化效应。
理解方位角有助于正确解读粒子碰撞、电磁散射、量子态分布等物理过程的角分布特征。
正确!散射角(θ)与方位角(ϕ)的类比:纬度与经度
您总结得非常准确!在球坐标系中,散射角和方位角的关系确实可以类比为地球的 纬度 和 经度:
| 概念 | 符号 | 范围 | 类比地理坐标 | 物理意义 |
|---|---|---|---|---|
| 散射角 | \( \theta \) | \( 0 \leq \theta \leq \pi \) | 纬度(从北极到南极) | 入射方向(\(z\)轴)与散射方向的夹角 |
| 方位角 | \( \phi \) | \( 0 \leq \phi < 2\pi \) | 经度(绕赤道旋转) | 散射方向在\(xy\)平面的投影与\(x\)轴的夹角 |
1. 几何图示
假设入射光子沿 \(z\)轴 运动,与电子发生散射:
- 散射角 \( \theta \):散射后的光子方向与\(z\)轴的夹角(类似纬度,决定能量损失)。
- \( \theta = 0^\circ \):前向散射(光子几乎不偏转)。
- \( \theta = 180^\circ \):后向散射(光子反向弹回)。
- 方位角 \( \phi \):散射方向在\(xy\)平面上的投影与\(x\)轴的夹角(类似经度,描述空间取向)。
- 通常对非偏振光求平均后,散射截面与\( \phi \)无关。
2. 物理意义对比
(1) 散射角 \( \theta \)
- 直接关联能量变化:
在康普顿散射中,光子波长偏移量由 \( \theta \) 决定: \[ \Delta\lambda = \frac{h}{m_e c} (1 - \cos\theta) \]- \( \theta \) 越大,光子能量损失越多(波长变长)。
- 微分截面的主要依赖:
例如汤姆逊散射的 \( \frac{d\sigma}{d\Omega} \propto (1 + \cos^2\theta) \)。
(2) 方位角 \( \phi \)
- 描述散射平面的取向:
若入射光为线偏振(如沿\(x\)轴),散射截面会显式依赖 \( \phi \): \[ \frac{d\sigma}{d\Omega} \propto \sin^2\phi \quad \text{(偏振光情况)} \] - 非偏振光中对称:
对 \( \phi \) 积分后,通常得到 \( 2\pi \) 的因子。
3. 实际应用中的简化
- 非偏振光散射:
由于各向同性,可直接对 \( \phi \) 积分,微分截面仅保留 \( \theta \) 依赖: \[ \frac{d\sigma}{d\Omega} = \frac{1}{2\pi} \int_0^{2\pi} \frac{d^2\sigma}{d\theta d\phi} d\phi \quad \Rightarrow \quad \text{仅含 } \theta \text{ 的表达式} \] - 偏振光分析:
需同时测量 \( \theta \) 和 \( \phi \) 以提取极化信息(如天体物理中的同步辐射偏振)。
4. 常见问题
Q1:为什么散射问题常选\(z\)轴为入射方向?
- 简化计算:入射方向沿坐标轴时,动量守恒的数学表达更简洁。
- 对称性:对非偏振光,绕\(z\)轴的旋转对称性允许忽略 \( \phi \) 的影响。
Q2:如何从实验数据中提取\( \theta \)和\( \phi \)?
- 探测器阵列:
例如高能物理实验中的电磁量能器,通过记录散射粒子的位置反推 \( (\theta, \phi) \)。 - 示例:
康普顿散射实验中,测量散射光子的能谱(反映 \( \theta \))和空间分布(反映 \( \phi \))。
5. 总结
- 散射角 \( \theta \) ≈ 纬度 → 决定散射的物理效应(如能量转移)。
- 方位角 \( \phi \) ≈ 经度 → 描述散射的空间取向(尤其在偏振分析中)。
- 核心公式:微分截面 \( \frac{d\sigma}{d\Omega} \) 通常先按 \( \theta \) 和 \( \phi \) 分解,再根据对称性简化。
这种类比不仅帮助直观理解角度参数的意义,也揭示了散射问题中方向分析的普适方法。
(知乎上找了张图):
1. 散射电场的经典计算
(1) 入射电磁波驱动电子运动
假设入射电磁波为单色平面波(沿 \( z \) 轴传播),电场为: \[ \mathbf{E}_{\text{inc}} = E_0 e^{i(kz - \omega t)} \hat{\mathbf{x}} \] 电子在电场中受洛伦兹力(非相对论近似,忽略磁场项): \[ m_e \frac{d^2 \mathbf{r}}{dt^2} = -e \mathbf{E}_{\text{inc}} \implies \mathbf{a}(t) = \frac{-e E_0}{m_e} e^{-i\omega t} \hat{\mathbf{x}} \]
(2) 辐射电场(李纳-维谢尔势)
加速电子在远场区(距离 \( r \gg \lambda \))辐射的电场为: \[ \mathbf{E}_{\text{scatt}} = \frac{e}{4\pi \epsilon_0 c^2 r} \left[ \mathbf{n} \times (\mathbf{n} \times \mathbf{a}) \right]_{\text{ret}} \] 其中 \( \mathbf{n} \) 为散射方向单位矢量。代入加速度 \( \mathbf{a} \): \[ \mathbf{E}_{\text{scatt}} \propto \frac{e^2 E_0}{m_e} \frac{1}{r} \left[ \mathbf{n} \times (\mathbf{n} \times \hat{\mathbf{x}}) \right] e^{i(kr - \omega t)} \]
2. 散射强度的计算
(1) 电场模平方
散射强度 \( I_{\text{scatt}} \propto |\mathbf{E}_{\text{scatt}}|^2 \),需计算: \[ |\mathbf{E}_{\text{scatt}}|^2 \propto \left| \mathbf{n} \times (\mathbf{n} \times \hat{\mathbf{x}}) \right|^2 \] 利用矢量恒等式 \( \mathbf{n} \times (\mathbf{n} \times \hat{\mathbf{x}}) = \hat{\mathbf{x}} - (\mathbf{n} \cdot \hat{\mathbf{x}}}) \mathbf{n} \),其模平方为: \[ \left| \hat{\mathbf{x}} - (\mathbf{n} \cdot \hat{\mathbf{x}}}) \mathbf{n} \right|^2 = 1 - (\mathbf{n} \cdot \hat{\mathbf{x}}})^2 = \sin^2 \chi \] 其中 \( \chi \) 是 \( \hat{\mathbf{x}} \) 与散射方向 \( \mathbf{n} \) 的夹角。
(2) 球坐标系下的角度关系
在球坐标系中,散射方向 \( \mathbf{n} \) 的极角为 \( \theta \)(散射角),方位角为 \( \phi \): \[ \mathbf{n} \cdot \hat{\mathbf{x}} = \sin\theta \cos\phi \] 因此: \[ |\mathbf{E}_{\text{scatt}}|^2 \propto 1 - \sin^2\theta \cos^2\phi \]
3. 非偏振光的方位角平均
对于非偏振入射光,电场方向随机分布(即 \( \hat{\mathbf{x}} \) 和 \( \hat{\mathbf{y}} \) 方向等概率),需对极化方向平均: \[ \langle |\mathbf{E}_{\text{scatt}}|^2 \rangle \propto \frac{1}{2} \left( (1 - \sin^2\theta \cos^2\phi) + (1 - \sin^2\theta \sin^2\phi) \right) \] 化简后: \[ \langle |\mathbf{E}_{\text{scatt}}|^2 \rangle \propto 1 - \frac{1}{2} \sin^2\theta (\cos^2\phi + \sin^2\phi) = 1 - \frac{1}{2}\sin^2\theta = \frac{1 + \cos^2\theta}{2} \]
方位角积分
由于结果已与 \( \phi \) 无关,对 \( \phi \) 积分仅产生因子 \( 2\pi \): \[ \int_0^{2\pi} \frac{1 + \cos^2\theta}{2} d\phi = \pi (1 + \cos^2\theta) \]
4. 与微分截面的关系
散射截面正比于散射强度,因此: \[ \frac{d\sigma}{d\Omega} \propto \langle |\mathbf{E}_{\text{scatt}}|^2 \rangle = \frac{r_e^2}{2} (1 + \cos^2\theta) \] 其中经典电子半径 \( r_e = \frac{e^2}{4\pi \epsilon_0 m_e c^2} \) 用于归一化。
5. 关键结论
- 散射强度: \[ |E_{\text{scatt}}|^2 \propto 1 - \sin^2\theta \cos^2\phi \quad (\text{单极化}) \] \[ \langle |E_{\text{scatt}}|^2 \rangle \propto \frac{1 + \cos^2\theta}{2} \quad (\text{非偏振光}) \]
- 方位角平均:
- 对非偏振光,天然隐含在极化方向的平均中。
- 显式积分 \( \phi \) 仅用于验证对称性(最终结果与 \( \phi \) 无关)。
- 总强度: 对立体角积分后得到总截面 \( \sigma_T = \frac{8\pi}{3} r_e^2 \)。
图示说明
z
| θ(散射角)
/
/
/
/_____ y
ϕ(方位角)
x
- \( \theta \) 决定能量分布,\( \phi \) 描述散射平面方向。
- 非偏振下 \( \phi \) 的对称性使得方位角平均简化为乘法因子。
此推导完整展示了从经典辐射理论到量子极限(汤姆逊散射)的自洽过程。
1. 为什么散射截面正比于散射场强的平方?
(1) 经典电动力学的辐射功率
根据经典电动力学,加速电荷(如被入射光电场驱动的电子)会辐射电磁波,其辐射功率由 坡印廷矢量(Poynting vector) 描述: \[ \mathbf{S}_{\text{scatt}} = \frac{1}{\mu_0} \mathbf{E}_{\text{scatt}} \times \mathbf{B}_{\text{scatt}} \propto |E_{\text{scatt}}|^2 \]
- 散射强度(单位面积的功率)直接正比于散射电场的平方 \( |E_{\text{scatt}}|^2 \)。
(2) 散射截面的定义
散射截面 \( \sigma \) 的物理意义是:
靶粒子(如电子)看起来有多大面积能有效拦截入射波并将其散射。
数学上定义为: \[ \sigma = \frac{\text{散射总功率}}{\text{入射波能流密度}} = \frac{\int |\mathbf{S}_{\text{scatt}}| , dA}{|\mathbf{S}_{\text{inc}}|} \] 由于 \( \mathbf{S}_{\text{scatt}} \propto |E_{\text{scatt}}|^2 \),且入射能流 \( \mathbf{S}_{\text{inc}} \propto |E_{\text{inc}}|^2 \),因此: \[ \sigma \propto \frac{|E_{\text{scatt}}|^2}{|E_{\text{inc}}|^2} \] 在固定入射场强下,\( \sigma \propto |E_{\text{scatt}}|^2 \)。
2. 散射场强就是辐射电场强度吗?
是的,散射场强 \( E_{\text{scatt}} \) 就是电子受迫振动后辐射的电场强度,但需注意以下两点:
(1) 经典与量子视角的统一
- 经典理论:\( E_{\text{scatt}} \) 是电子加速运动辐射的电场(由李纳-维谢尔势计算)。
- 量子理论:散射场是入射光子与电子相互作用后重新辐射的量子场,其振幅对应经典 \( E_{\text{scatt}} \)。
(2) 场强的物理意义
- \( |E_{\text{scatt}}|^2 \) 表征散射光的 概率密度(量子)或 能流密度(经典)。
- 在量子电动力学(QED)中,散射截面通过费曼图振幅 \( \mathcal{M} \) 计算,而 \( |\mathcal{M}|^2 \propto |E_{\text{scatt}}|^2 \)。
3. 具体到汤姆逊散射的推导
(1) 散射电场的计算
入射电场 \( \mathbf{E}_{\text{inc}} \) 驱动电子运动,电子加速度 \( \mathbf{a} = -e \mathbf{E}_{\text{inc}} / m_e \)。辐射电场为: \[ \mathbf{E}_{\text{scatt}} \propto \frac{e \mathbf{a}}{r} \implies |E_{\text{scatt}}| \propto \frac{e^2 |E_{\text{inc}}|}{m_e r} \]
(2) 微分截面的表达式
散射截面正比于散射与入射场强的比值平方: \[ \frac{d\sigma}{d\Omega} \propto \left| \frac{E_{\text{scatt}}}{E_{\text{inc}}} \right|^2 \propto \left( \frac{e^2}{m_e} \right)^2 = r_e^2 \] 结合角度依赖后得到: \[ \frac{d\sigma}{d\Omega} = \frac{r_e^2}{2} (1 + \cos^2 \theta) \]
4. 量子与经典的对应关系
| 量 | 经典理论 | 量子理论 |
|---|---|---|
| 散射场强 | \( E_{\text{scatt}} \) | 光子辐射振幅 \( \mathcal{M} \) |
| 截面正比于 | \( | E_{\text{scatt}} |
| 物理本质 | 电磁波辐射功率 | 散射概率幅的平方 |
5. 常见疑问解答
Q1:为什么不是 \( \sigma \propto |E_{\text{scatt}}| \)?
- 截面反映的是 概率 或 功率,而功率总与场的平方相关(能量密度 \( \propto |E|^2 \))。
Q2:康普顿散射是否也适用?
- 是的!Klein-Nishina公式中 \( \frac{d\sigma}{d\Omega} \propto |\mathcal{M}|^2 \),量子振幅 \( \mathcal{M} \) 对应经典 \( E_{\text{scatt}} \)。
总结
- 散射截面正比于 \( |E_{\text{scatt}}|^2 \),因为截面本质描述的是散射能量的相对强度。
- 散射场强 \( E_{\text{scatt}} \) 是电子辐射的电场,经典与量子理论通过不同方式描述同一物理量。
- 这一关系在从经典汤姆逊散射到量子康普顿散射中均成立,体现了电磁相互作用的普适性。