我们使用几何来解释洛伦兹变换。
在运动坐标系\(O’\) 中,向垂直方向\(y\)方向发射一个光子,到达点(事件)\(P’\),如图:
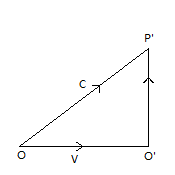
那么在静止坐标系\(O\)中发射一个光子到\(P’\),走过的路程\(OP’\),在O看来,O’中光走过的距离\(OP’\)为\(OP\)的\(\gamma=1/\sqrt{1-v^2/c^2}\)倍
因为水平方向的速度是\(v\),垂直方向是\( c \),所以很容易得到\(OP’\)为\(OP\)的\(\gamma=1/\sqrt{1-v^2/c^2}\)倍。但因为光速不变,所以在\(O\)坐标看来,\(O\)的坐标系的时间必须同时放大 \(\gamma\)倍,才能保持光速为\(c\),所以\(t=\gamma t’\)。
现在看从\(O’\)坐标系,在原点同时发射一束垂直光线和一束水平光线,分别沿着到\(y\)轴和\(x\)轴前进:当\(x\)轴的光子走了距离\(x’\)时,\(y\)轴上的到达点\(P’\),走了距离\(y’=x’\):
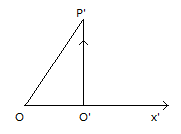
从前面的分析得出,在坐标系\(O\)看来,\(y’\)的长度会变成\(y=\gamma y’\),扩大了\(\gamma\)倍,为了保持光速不变,时间也必须同时扩大\(\gamma\)倍。
为了保持测到的物体形状不变,\(x\)方向上的距离数据,必须同比例放大,所以测得的x’也会放到到\(\gamma x’\),\(O\)坐标系上的\(x\)值,对应着\(O’\)坐标系上的\(x’+vt’\),所以就有\(x=\gamma(x’+vt’)\)
\(O’\)上\(x’+vt’\)这段距离,光通过这段距离,需要的时间为\( \frac{x’}{c}+\frac{vt’}{c}=t’+\frac{vx’/c}{c}=t’+\frac{vx’}{c^2}\),由于测得的t应该扩大\(\gamma\)倍,所以\(t=\gamma(t’+\frac{vx’}{c^2})\)
进一步分析,我们会发现,实际上,\(O\)坐标系使用了自己的时间尺度来计算\(O’\)坐标系内光走的距离,导致了看起来\(O’\)坐标系的光速只有\(O\)坐标系的\(\sqrt{1-v^2/c^2}\),实际上\(O’\)上自己的时间尺度,和\(O\)是完全一样的,使用自己的坐标系时间尺度来看另一个坐标系,由于角度不同就会出现光速不同从而导致时间尺度也不同了。
我们也可以这样理解: 在O’上垂直发射一束光线,那么在O上看来,由于水平方向存在速度v,那么O’上的光线必然会有一个分量速度v,而垂直方向上的光速就不能是c了,否则两者合成速度就是\(\sqrt{c^2+v^2}\)了,那么垂直方向的光速只能是\(\sqrt{c^2-v^2}\),这样和v的合成速度就是c了。这也提醒了我们,这种情况下,光子就变成了有静质量的粒子了,似乎被束缚了。
所以,通过几何方式得到洛伦兹变换,我们基于以下几点:
- 使用自己坐标内的时间尺度来估算对方坐标系的物理量
- 光速不变
- 物体在不同坐标系内等比例缩放(各向同性)
- 洛伦兹变换出现的根本原因,在于不同坐标系观察同一事件的距离和时间的不同,但并未使用对方的物理量来计算