以前证明洛伦兹变换,都是使用的直角三角形,而没有使用斜线的方式。
现在我们考虑斜线的方式,其实也要使用直角三角形,如下图:
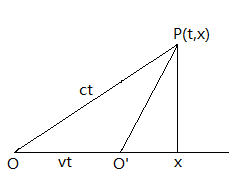
图中,从O随意发射一束光线,经过时间t,到达点\(P(t,x)\),P点在x轴上的投影为\(x\),此时O’坐标系走了\(vt\),在O’坐标系中,P点在O’的x轴的投影值为\(x’\), 从O’到P点光走的距离为\(ct’\)
我们需要分段求从x到\(x’+vt’\)的关系,先求\(vt\)和\(vt’\)的关系,再求\(x-vt\)和\(x’\)的关系。
我们首先把ct线段OP拉到点q,使得O’q垂直于x轴(ct’也同步变化),Oq=ct,如下图:
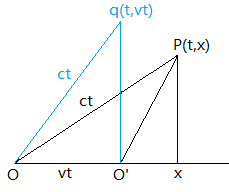
此时,我们很容易证明\(vt=\gamma vt’\):
此时,\(x=vt\),\(x’=0\),根据\((ct)^2 -x^2 =(ct’)^2 -x’^2\),可得:
\(t=\gamma t’\),于是有:
\( vt=\gamma vt’ \)
然后我们再求\(x-vt\)与\(x’\)的关系,因为是对应关系,所以也应该是\((x-vt)=\gamma x’ \)
我们也把当前的O’作为O的原点,把O’P拉到O’q和x-vt成c/v比例的直角三角形\((O’q/(x-vt)=c/v)\),对应的ct’也做相应的变化,如下图:
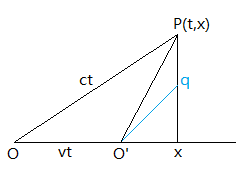
使用式子 \((ct)^2-x^2=(ct’)^2-x’^2\)
此时\(ct=>O’q=(x-vt)*c/v\),\(ct’=>x’*c/v\),而式子中的x’此时对应着0 (q在O’上的投影为0),所以有:
\( ((x-vt)*c/v)^2 -(x-vt)^2 =(x’*c/v)^2 -0 \),于是可以得到:
\( (x-vt) =\gamma x’ \),于是有:
\( x =\gamma x’ + vt =\gamma x’ + \gamma vt’ =\gamma (x’+vt’)\)